Lesson: Chapter - 5

Polynomials

A polynomial is an expression that contains one or more algebraic terms, each consisting of a constant multiplied by a variable raised to a power greater than or equal to zero. For example, x² + 2 x + 4 ,is a polynomial with three terms (the third term is 4 x⁰ = 4 . 2 x^-1 on the other hand, is not a polynomial because x is raised to a negative power. A binomial is a polynomial with exactly two terms:x + 5 and x² - 6 are both binomials.

The rest of this chapter will show you how to perform different operations on and with polynomials.

Multiplying Binomials

There is a very simple acronym that is useful in remembering how to multiply binomials. It is FOIL, and it stands for First, Outer, Inner, Last. This is the order that you multiply the terms of two binomials to get the right product.

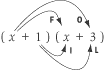
For example, if asked to multiply the binomials: (x + 1) (x + 3) You first multiply the first terms of each binomial: x × x = x ² Next, multiply the outer terms of the binomials: x × 3 = 3x Then, multiply the inner terms: 1 × x = x Finally, multiply the last terms: 3 × -2 = -6 Combine like terms and you have your product: 2x² + -2x + 6x+ -6 = 2x² + 4x - 6 Here are a few more examples:

Multiplying Polynomials

Every once in a while, the Math IC test will ask you to multiply polynomials. It may seem like a daunting task. But when the process is broken down, multiplying polynomials requires nothing more than distribution and combining like terms.

Consider the polynomials (a + b + c) and (d + e + f). To find their product, just distribute the terms of the first polynomial into the second polynomial individually and combine like terms to formulate your final answer:

Here’s another example:

As you can see, multiplying polynomials is little more than rote multiplication and addition.

Video Lesson - Solving Quadratic Equation

Quadratic Equations

A quadratic, or quadratic polynomial, is a polynomial of the form ax² + bx + c, where a ? 0. The following polynomials are quadratics:

A quadratic equation sets a quadratic polynomial equal to zero. That is, a quadratic equation is an equation of the form ax² + bx + c = 0. The values of x for which the equation holds are called the roots, or solutions, of the quadratic equation. Most of the questions on quadratic equations involve finding their roots.

There are two basic ways to find roots: by factoring and by using the quadratic fo-rmula. Factoring is faster, but it can’t always be done. The quadratic formula takes longer to work out, but it works for all quadratic equations. We’ll study both in detail.

Factoring

To factor a quadratic, you must express it as the product of two binomials. In essence, factoring a quadratic involves a reverse-FOIL process. Take a look at this quadratic:

x² + 10 x + 21

In the example above, the leading term has a coefficient of 1 (since 1x² is the same as x²). Since the two x variables are multiplied together during the FIRST step of foiling to get the first term of the quadratic polynomial, we know that the binomials whose product is this quadratic must be of the form (x + m)(x + n), where m and n are constants. You also know that the sum of m and n is 10, since the 10x is derived from multiplying the OUTER and INNER terms of the binomials and then adding the resulting terms together (10x = mx + nx, so m + n must equal 10). Finally, you know that the product of m and n equals 21, since 21 is the product of the two last terms of the binomials.

Now you just need to put the pieces together to find the values of m and n. You know that x is the first term of both binomials, and you know that the sum of m and n is 10 and the product of m and n is 21. The pair of numbers that fit the bill for m and n are 3 and 7. Thus, x² + 10x + 21 = (x + 3)(x + 7). The quadratic expression has now been factored and simplified.

On the test, though, you will often be presented with a quadratic equation. The only difference between a quadratic equation and a quadratic expression is that the equation is set equal to 0 (x² + 10x + 21 = 0). If you have such an equation, then once you have factored the quadratic you can solve it. Because the product of two terms is zero, one of the terms must be equal to zero. Thus, since x + 3 = 0 or x + 7 = 0, the solutions (also known as the roots) of the quadratic must be x = –3 and x = –7.

Quadratics with Negative Terms

So far we’ve dealt only with quadratics in which the terms are all positive. Factoring a quadratic that has negative terms is no more difficult, but it might take slightly longer to get the hang of it, simply because you are less used to thinking about negative numbers.

Consider the quadratic equation x² – 4x – 21 = 0. There are a number of things you can tell from this equation: the first term of each binomial is x, since the first term of the quadratic is x²; the product of m and n is –21; and the sum of a and b equals –4. The equation also tells you that either m or n must be negative but that both cannot be negative, because the multiplication of one positive and one negative number can only result in a negative number. Now you need to look for the numbers that fit these requirements for m and n. The numbers that multiply together to give you –21 are: –21 and 1, –7 and 3, 3 and –7, and 21 and –1. The pair that works in the equation is –7 and 3.

Two Special Quadratic Polynomials

There are two special quadratic polynomials that pop up quite frequently on the Math IC, and you should memorize them. They are the perfect square and the difference of two squares. If you memorize the formulas below, you may be able to avoid the time taken by factoring.

There are two kinds of perfect square quadratics. They are:

1. a² + 2ab + b² = (a + b)(a + b) = (a + b)². Example: a² + 6ab + 9 = (a + 3)²
2. a² – 2ab + b² = (a – b)(a – b) = (a – b)². Example: a² – 6ab + 9 = (a –3)²

Note that when you solve for the roots of a perfect square quadratic equation, the solution for the equation (a + b)² = 0 will be –b, while the solution for (a + b)² = 0 will be b.

The difference of two squares quadratics follow the form below: (a + b)(a - b)=(a² - b²) Examples: (a + 3)(a - 3)=(a² - 9

Here’s an instance where knowing the perfect square or difference of two square equations can help you:

Solve for x: 2x² + 20x + 50 = 0. To solve this problem by working out the math, you would do the following:

If you got to the step where you had 2(x² + 10x +25) = 0 and realized that you were working with a perfect square of 2(x + 5)², you could immediately have divided out the 2 from both sides of the equation and seen that the solution to the problem is –5.

Practice Quadratics

Since the ability to factor quadratics relies in large part on your ability to “read” the information in the quadratic, the best way to get good is to practice, practice, practice. Just like perfecting a jump shot, repeating the same drill over and over again will make you faster and more accurate. Take a look at the following examples and try to factor them on your own before you peek at the answers.

The Quadratic Formula

Factoring using the reverse-FOIL method is really only practical when the roots are integers. Quadratics, however, can have decimal numbers or fractions as roots. Equations like these can be solved using the quadratic formula. For an equation of the form ax² + bx + c = 0, the quadratic formula states:

Consider the quadratic equation x² + 5x + 3 = 0. There are no integers with a sum of 5 and product of 3. So, this quadratic can’t be factored, and we must resort to the quadratic equation. We plug the values, a = 1, b = 5, and c = 3 into the formula:

The roots of the quadratic are approximately {–4.303, –.697}.

Finding the Discriminant:

If you want to find out quickly how many roots an equation has without calculating the entire formula, all you need to find is an equation’s discriminant. The discriminant of a quadratic is the quantity b² – 4ac. As you can see, this is the radicand in the quadratic equation. If:

1. b² – 4ac = 0, the quadratic has one real root and is a perfect square.
2. b² – 4ac > 0, the quadratic has two real roots.
3. b² – 4ac < 0, the quadratic has no real roots, and two complex roots.

This information is useful when deciding whether to crank out the quadratic formula on an equation, and it can spare you some unnecessary computation. For example, say you’re trying to solve for the speed of a train in a rate problem, and you find that the discriminant is less than zero. This means that there are no real roots (a train can only travel at speeds that are real numbers), and there is no reason to carry out the quadratic formula.

Next to display next topic in the chapter.

Mathematics Practice Questions