What if we are asked to find the distance between
two points on the coordinate plane that do not share a coordinate?
We have to use another approach.
First, we draw a right triangle, setting the
distance between the two points to be the hypotenuse.
We then use the Pythagorean theorem and our knowledge of triangles
to find the length of that hypotenuse.
Task: Let's find the distance between the points
(–5, – 3) and (7, –12). We can draw lines perpendicular
to the x and y-axes, plus one directly between
the points, to create a right triangle. Now, use what you've
just learned to find the distances between the points that
share coordinates. These are the legs of the triangle. Then,
use your knowledge of triangles to find the answer. Type in
your answer, and then click Continue.
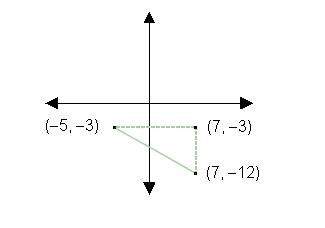
Countinue
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.