Lesson: Geometry Challenging - 23t01

Distances On The Coordinate Plane, continued

What if we are asked to find the distance between two points on the coordinate plane that do not share a coordinate? We have to use another approach.

First, we draw a right triangle, setting the distance between the two points to be the hypotenuse.

We then use the Pythagorean theorem and our knowledge of triangles to find the length of that hypotenuse.

Task: Let's find the distance between the points (5,– 3) and (7, –12). We can draw lines perpendicular to the x and y-axes, plus one directly between the points, to create a right triangle. Now, use what you've just learned to find the distances between the points that share coordinates. These are the legs of the triangle. Then, use your knowledge of triangles to find the answer. Type in your answer, and then click Continue.

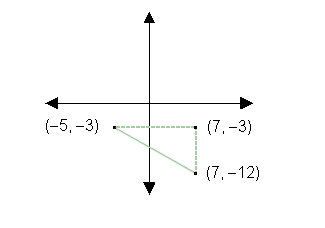
Distance between (–5, –3) and (7, –12) = 15

First, find the distances that make up the legs of the triangle. The distance from (–5, –3) to (7, –3) is 5+7=12. The distance from (7, –3) to (7, –12) is 12 – 3 = 9. Now, we could use the Pythagorean theorem to get the hypotenuse. But, if we recognize that we have a 3:4:5 ratio, we save ourselves the work! The legs of 9 and 12 are products of 3 times 3, and of 3 and 4, respectively, so our hypotenuse must be the product of 3 and 5, or 15.

Next to display next topic in the chapter.