Task: Select the correct answer and then click Continue.
In the figure above, P is the center
of the two circles. If 
,
what is the area of the shaded region?
To answer this question, we must first find the area of the large
circle and the area of the small circle. Once we have these values,
we can then subtract the smaller area from the larger to obtain
the area of the shaded region.
The diagram indicates that the large circle has a radius of
length y. Therefore its area 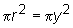is 
.
Likewise, the small circle has a radius of length x,
so its area is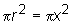 
,
and the difference between the two areas is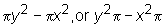 
.
However, the question stem tells us that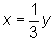 
,
and the answer choices are expressed in terms of x
alone. Re–expressing y in terms of x,
we get 
.
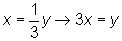Substituting 3x into the expression above, we can determine
the area of the shaded region:
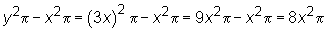
Choice (C) is correct.
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.