Practice Finding the Trigonometric Ratios

Practice Finding the Trigonometric Ratios

So you know what sine, cosine and tangent are. Great! But how do you use them? Find out how in this lesson as we find missing sides and angles using trigonometric ratios.

Trigonometric Ratios

Meet X. X is suffering from amnesia. X isn't even her real name. All she knows is she's on this right triangle.

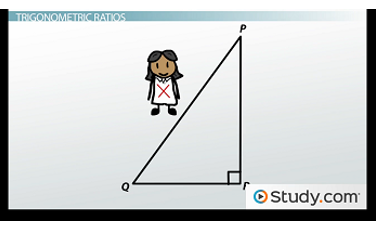
Can we help X find out her identity? Let's see. Can we use the Pythagorean theorem? Well, we can use that to find the missing side of a right triangle, but we need to know the other two sides. We only know that QR is 7. And let's just say 7 isn't very friendly. There's a rumor that 7 ate 9, which worries X.

What about angle Q? We know that's 63 degrees. Is that useful? It is, but only if we know how to use trigonometric ratios. The trigonometric ratios we're going to focus on here are sine, cosine and tangent. These are like the Moe, Larry, and Curly of trigonometry. Sure, there are other Stooges, but these are the best.

Let's define them. To start, let's label the sides of this triangle. X is on PQ, the longest side and the side opposite the right angle. We call that the hypotenuse. If we're talking in terms of angle Q, then QR is called the adjacent side. PR is the opposite side. They're adjacent and opposite to the angle in question.

Note that the hypotenuse is always the same, but if we were focusing on a different angle, the other labels would change. For example, if we knew angle P, then PR would be the adjacent side and QR would be the opposite side. Ok, fear not, X, we're almost there.

Let's get to our ratios. First, sine is opposite/hypotenuse, which we write as sin? = opposite/hypotenuse. We're going to use ? to stand in for the angle. Next, cosine is adjacent/hypotenuse. We write this as cos? = adjacent/hypotenuse. Finally, tangent is opposite/adjacent, which we write as tan? = opposite/adjacent. We can remember these with the acronym SOH CAH TOA.

Solving for a Side

So how do we use this? You'll usually be asked to find a missing side or angle in a right triangle by using these trigonometric ratios. With X, we're missing a side length. Which side? The hypotenuse. Okay, which of our trig functions uses the hypotenuse? SOH CAH TOA. SOH and CAH have that H, so sine or cosine is what we need.

What else do we know? We know QR, which is adjacent to the angle we know. Sine or cosine - which uses the adjacent? CAH, that's cosine. Cosine is adjacent over hypotenuse. So we can set up our equation like this: cos(63) = 7/x.

X is a little nervous about being so close to 7, but thankful that she's almost figured out her identity. Okay, what's the cosine of 63? If we use our calculator, we find out that cosine of 63 is .454. Remember to be sure your calculator is set to degrees, not radians.

So .454 = 7/x. Let's cross multiply to get .454x = 7. Then divide both sides by .454 to get x = 15.4, so that's what xis! 15.4. We did it. X is a mystery no longer.

Practice Problem

Sometimes, these problems aren't as easily formatted. Here's what they might look like: In triangle DEF, hypotenuse DE = 12, and angle D = 38 degrees. Find the length of EF, to the nearest tenth.

Well, the first thing we should do is bust out our art skills and draw this triangle. You can put your protractor away; it doesn't need to be exact. This will do.

Let's label what we know. DE, our hypotenuse, is 12. And angle D is 38 degrees. We want to find EF, so let's label that x. Another amnesia victim? Man, this lesson has more amnesia victims than a soap opera.

What do we do? Well, if D is our ?, we want to find the side opposite. What do we already know? The hypotenuse. Which part of SOH CAH TOA uses the opposite and hypotenuse? Sine! So we set up our equation: sin(38) = x/12. Let's use our calculator to find out what the sine of 38 is. It looks like it's 0.616.

So 0.616 = x/12. Now we multiply both sides by 12, and x = 7.392. Our problem said round to the nearest tenth, so our final answer is 7.4. EF = 7.4. Another amnesia case solved.

Solving for an Angle

If this is a soap opera, then you never know where amnesia will strike. Sometimes it's on a side; sometimes it's on an angle. It does always seem to be convenient for the plot, though. And this lesson is no exception.

Here's a problem: In triangle JKL, leg JL = 9 and leg KL = 22. Find angle J, to the nearest degree. Just when we needed to practice finding a missing angle, amnesia strikes an angle. Go figure. Anyway, let's draw. Here's triangle JKL. No need to be exact. We know JL is pretty short relative to KL. We can label JL as 9 and KL as 22. And what do we want to find? Angle J. Let's label that as yet another x.

Ok, SOH CAH TOA time. If J is our angle in question, what is JL? It's the adjacent side. And what is KL? The opposite side. Which part of SOH CAH TOA uses the opposite and adjacent? Tangent!

So tan(x) = 22/9. What is 22 divided by 9? Well, it's 2.444 repeating.

Well, jeez. How do we find out what x is? We need the inverse tangent. This is the tangent with that little -1 exponent. On most scientific calculators, you can enter your number, so 2.444 here, then hit the inverse tangent button. If we do this, we get 67.747. Rounding, that's 68 degrees. So angle J is 68 degrees. And that's it!

Lesson Summary

We learned that amnesia can strike anyone at any time, especially in soap operas and trigonometry lessons. More importantly, we used trigonometric functions to find missing sides and angles in right triangles.

The trigonometric ratios are sine, cosine and tangent. We remember these with the acronym SOH CAH TOA. That's sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, and tangent = opposite/adjacent.

To find the missing side or angle, we just determine which ratio to use, plug in what we know, and solve!