Formula for the Area of an Ellipse

Formula for the Area of an Ellipse

In this lesson, you'll learn some ellipse terminology. You'll also learn the formula for the area of an ellipse and go through a few examples of the equation in action. Then, you can test your new knowledge with a brief quiz.

What is an Ellipse?

An ellipse is an oval that is symmetrical along its shortest and longest diameters.

The ellipse is symmetrical along both blue lines.

This is an important distinction to make because not all ovals are ellipses.

This oval is not an ellipse.

The above oval, for example, is symmetrical along the blue line, but not along the red line because it bulges on its right end.

A true ellipse, however, is always symmetrical along its longest and shortest diameters. The longest diameter is called the major axis, and the shortest diameter is called the minor axis.

The lines of symmetry are also the axes.

If you halve these axes to create the ellipse's longest and shortest radii, you'll have the ellipse's semi-axes. The longer one is called the semi-major axis, and the shorter one is called the semi-minor axis. The semi-axes are always one-half the length of their corresponding whole axes.

Half of the axes of an ellipse are its semi-axes.

Area of an Ellipse

The formula for an ellipse's area is

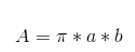
Where a and b are the lengths of the semi-major and semi-minor axes.

Let's apply the formula to a specific ellipse:

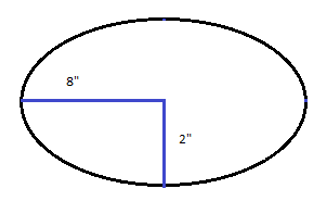
The length of this ellipse's semi-major axis is 8 inches, and the length of its semi-minor axis is 2 inches. We can plug these values into our area formula. I will approximate pi to 3.14 for the rest of the lesson.

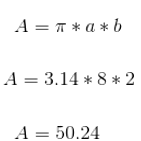
This ellipse's area is 50.24 square inches.

What if we're given an ellipse's area and the length of one of its semi-axes?

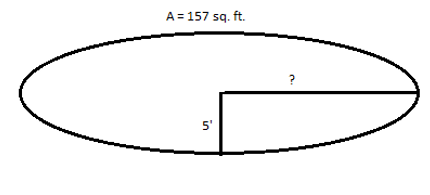
In this case, we know the ellipse's area and the length of its semi-minor axis. We can plug those values into the formula:

The length of the semi-major axis is 10 feet.

Dealing with Whole Axes

Let's find the area of the following ellipse:

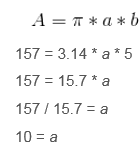
This diagram gives us the length of the ellipse's whole axes. But remember that an ellipse's semi-axes are half as long as its whole axes.

Since the major axis is 8 inches long, the semi-major axis is half that length, or 4 inches long. Likewise, since the minor axis is 6 inches long, the semi-minor axis is 3 inches long.

Now we can plug the semi-axes' lengths into our area formula:

This ellipse's area is 37.68 square inches.

Let's solve one more example. Given the ellipse below, what's the length of its minor axis?

The major axis is 24 meters long, so its semi-major axis is half that length, or 12 meters long. Using that information and the area, we can find the length of the semi-minor axis:

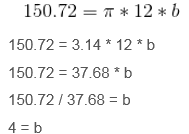
But we're not done! We've found the length of the ellipse's semi-minor axis, but the problem asks for the length of the minor axis. The minor axis is twice the length of the semi-minor axis. 4 * 2 = 8. So the minor axis's length is 8 meters.

Review

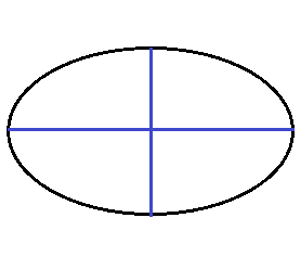
• An ellipse is an oval that is symmetrical along its longest and shortest diameters.
• An ellipse's longest diameter is its major axis.
• An ellipse's shortest diameter is its minor axis.
• An ellipse's longest radius, also half its major axis, is called its semi-major axis.
• An ellipse's shortest radius, also half its minor axis, is called its semi-minor axis.