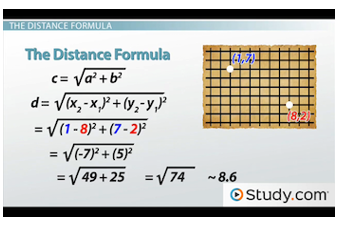
Applying the distance formula
(x2 - x1) would just be (1 - 8), and (y2 - y1) would be (7 - 2). Those two little problems give us -7 and 5, and then squaring both those numbers gives us 49 and 25. Look familiar? Adding those two together gives us 74, and then taking the square root finally leaves us with 8.6, just like before.
The only difference between this way and the Pythagorean Theorem was that we had a -7 for a few steps doing it this way, whereas it was a +7 before. That will happen a lot of the time, but it doesn't matter, because when we multiply it by itself (when we square it), it turns positive anyway; the negative goes away.
And, that's it! That's the distance formula. Let's just try a few quick examples with the formula to give you a little practice.
Example 1
You'll usually see the problems stated like this: Find the distance between the points (5, 9) and (-2, 3). Now, we could just graph these two points, go straight over and straight up to make a triangle, and then use a^2 + b^2 to find c^2, like the Pythagorean Theorem, but let's get some practice using the distance formula instead.
We'll start by identifying x1, x2, y1 and y2. x1 is the first x value and x2 the second; same thing for the ys. Now we plug these values into their places in the formula, giving us this: d = sqrt((5 - (-2))^2 + (9 - 3)^2). Doing the subtraction leaves us with 7 and 6. Then, squaring these numbers turns them into 49 and 36. Adding them together makes 85, and then taking the square root gives us our answer as around 9.2.
Example 2
Not too bad, right? Let's do one more for good measure. Find the distance between (-2, -1) and (2, -4). Again, start by identifying x1, x2, y1 and y2. Then, substitute them into the formula: d = sqrt((2 - (-2))^2 + ((-4) - (-1))^2). This time, we've got to be extra careful with our negatives. 2 - (-2) is like 2 + 2, so that gives us 4, and -4 - (-1) is like -4 + 1, which is -3. That leaves us here, with 4 squared and -3 squared on the inside of the square root. These turn into 16 and 9, which add together to 25, and the square root of 25 is just plain old 5.
Lesson Summary
And, that's the distance formula! Let's quickly review what we've learned. The distance formula is a condensed version of the Pythagorean Theorem (a^2 + b^2 = c^2) and looks like this: d = sqrt((x2 - x1)^2 + (y2 - y1)^2). x1, x2, y1 and y2 are just the x and y coordinates of these two points. And finally, be careful when you have to plug negatives into the distance formula. Sometimes two negatives make a positive.