Negative Exponent:

Negative Exponent: Definition & Rules

Negative exponents have caused problems for math students as long as they have been defined. This lesson will shed some light on the negative exponent: what it means and how to work with it in a math problem.

What are Exponents?

Exponents are numbers that are written as a superscript. The exponent tells a mathematician how many times a certain number should be multiplied to itself. For example:

2^3 = 2*2 *2 = 8

The word exponent is from the Latin expo, meaning out of, and ponere, meaning place. The first recorded modern usage of the concept was in the 1500's. However, the concept of squared and cubed numbers dates back to ancient Babylon.

Exponents are useful mathematical and scientific shorthand. Where it would be very confusing to try and perform mathematical calculations with numbers such as 602,000,000,000,000,000,000,000, it becomes not so bad if the number is written as 6.02*10^23.

Negative Exponents

Negative exponents are exactly what they are named; they are exponents that happen to be negative.

2^-3

In mathematics, this is not proper form for writing a number with an exponent, so the expression must be rewritten in its proper form.

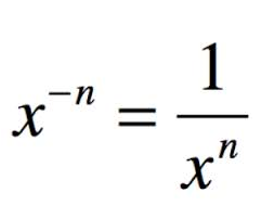
The best way to remember how to deal with a negative exponent is to remember that negative is the opposite of positive and division is the opposite of multiplication, so a number with a negative exponent should be moved to the denominator of a fraction and the exponent switched to positive. The opposite is also true. If the negative exponent is in the denominator of a fraction, its expression gets moved to the numerator and the sign of the exponent is changed.

That way

2^-3

becomes

1/2^3

What about something more complicated?

-5y^-3 z^5

becomes

-5z^5/y^3

And

2x^-3/y^2 z^-2

is

2z^2/x^3 y^2

Working with Negative Exponents

The rules of exponents, especially the product rule, still apply even if you are working with negative exponents.

Here is an example problem:

Another example:

x^2/x^7 = x^-5 = 1/x^5

Real Life Applications

As previously mentioned, there are many places in math and science where exponents are used to avoid extremely large or extremely small numbers. There are also instances where negative exponents are necessary. Determining the rate of nuclear decay of an isotope requires the use of negative exponents, as does figuring out how much money your retirement account has lost. Carbon dating is another area where negative exponents are involved.

Example

Nuclear energy derived from radioactive isotopes can be used to supply power to space vehicles. Suppose that the output of the radioactive power supply for a certain satellite is given by the function:

In the function f(x) is measured in watts and t is time in days, what will be the watts of power remaining after 250 days?

First, substitute the given values in the equation.

f(x) = 30e^-0.003(250)

Then solve

f(x) = 14.1 watts

Lesson Summary

Let's review:

Negative exponents are exactly what they are named. They are exponents that happen to be negative. An expression written with one or more negative exponents is not written in proper form, and must be rewritten. To do this, the expression with the negative exponent is moved to the denominator of a fraction and the exponent is written as a positive. Before completing any mathematical problem, look for negative exponents and convert them to their proper form.