Set Notation, Compound Inequalities, and Systems of Inequalities

Set Notation, Compound Inequalities, and Systems of Inequalities

In this lesson, we'll explore the conditions of compound inequalities and learn how to express them using set notation and interval notation. Test you knowledge afterward with a short quiz.

Understanding Inequalities

We've learned that an inequality is just an equation that has a greater than or less than symbol instead of an equals sign, and they help us say things like 'I need at least an 80% to get a B on my history test' or 'the amount of money I spend on video games and plane tickets has to be less than $3,000.' The first example was a 1-variable inequality because the only topic being discussed was the one test score, while the second was a 2-variable inequality because there were video games and plane tickets involved.

Compound Inequalities

But it's sometimes going to be the case that we want to be more specific than these last two examples. Instead of saying 'I need at least an 80% for a B,' it would actually be more accurate to say 'I need between an 80% and a 90% to get a B.' When we change 'greater than 80' into 'between 80 and 90,' we change this single inequality into a compound inequality because it now has two conditions: x = 80 and x < 90. In this case, for a number, x, to be part of the solution, both conditions must be satisfied. For example, a 92 is greater than or equal to 80, but it is not less than 90. Therefore, it's not a B.

This also changes our graph from a single dot with an arrow going forever in one direction, to two dots with a line segment connecting them. We get this picture by graphing one inequality at a time and then seeing where the two graphs overlap. We can start by graphing x = 80. We put a closed circle at 80 and draw an arrow going to the right to indicate that the answer could be any number 80 or larger. Next, we graph x < 90 by putting an open circle at 90 and drawing an arrow going to the left to indicate that the answer can be any number smaller than 90. But we then have to remember that the solution is the space where they are both true. This means the only part of the graph we want is where they overlap, and what we end up with is a line connecting our two points. A compound inequality where both conditions must be satisfied is called an 'and' compound inequality and will have a graph with a single interval, like this.

But we can also have what are called 'or' compound inequalities. For example, if, instead, we were describing the different ways I could get something other than a B, we would want to say that I could get less than an 80 or greater than or equal to 90. Now, instead of having to satisfy both conditions like before, the answer can satisfy either and still be okay. Getting less than 80 is one way to not get a B, but getting 90 or above is another way. They both work.

For example, a 72% is less than 80, so it's not a B. It doesn't matter that it isn't also greater than 90. It only has to satisfy one of the conditions. This means that our graph is a little bit different as well. It will again be two arrows, but this time we won't need them to overlap. We can put an open circle at 80 and draw our arrow to the left showing that all values less than 80 are included. Then, we can put a closed circle at 90 and draw our arrow to the right to show that all values greater than or equal to 90 are included. Again, we're not worried about where these graphs overlap because satisfying either one of these conditions is enough; they don't have to satisfy both to not be a B. A compound inequality where only one condition must be satisfied is called an 'or' compound inequality and will have a graph with two intervals that looks like this:

Set Notation and Interval Notation

Before we move on, let's talk about two mathematical notations commonly used to describe the solution sets of compound inequalities. The first is called set notation. If we were to write the solution set to our 'and' compound inequality in set notation, it would look something like this:

{x | x > 80 and x < 90}

What this literally says is that the solution set is all values of x, such that x is greater than or equal to 80 and less than 90. In case you were wondering, the vertical line symbol, |, is translated as the phrase 'such that.' You might see a colon used instead of the vertical line sometimes, but they mean the exact same thing. The solution set of an 'or' compound inequality is written in the same way, but with the word 'or' used instead of 'and':

{x | x < 80 or x > 90}

This says that the solution set is all values of x, such that x is less than 80 or greater than or equal to 90.

Moving on, the second notation we can use is called interval notation. This notation is especially compact and used more often than set notation for expressing solution sets of compound inequalities. For example, the answer to our 'and' compound inequality could be expressed using interval notation like this: [80,90)

The first number is the lower bound, and the second is the upper bound. The opening bracket, [, indicates that 80 is included in the solution and is equivalent to saying greater than or equal to. The closing parenthesis on the other end, ), indicates that 90 is not included in the solution and is the same as saying less than.

Expressing the solution to 'or' compound inequalities is a little more complicated because there are two intervals in the solution instead of one. If we expressed the solution to our previous example of how not to get a B, it would like this: [0, 80) U [90,100]

The symbol, U, in the middle stands for union and means that both sets are part of the solution. The first set says that anything from 0 up to, but not including 80, is not a B, and the last tells us that anything from 90 to 100 is also not a B. Again, the numbers tell us the bounds, and the brackets and parentheses tell us whether the bound is, or is not, part of the solution.

System of Inequalities

Just like we can have multiple 1-variable inequalities in a single problem, we can have multiple 2-variable inequalities in a single problem as well. When this happens, it's called a system of inequalities.

We can graph a system of inequalities by working with one inequality at a time. For example, what if we were asked to find the area of the graph where both of the following inequalities were true?

We would begin by graphing the first inequality, y > x + 1, on our coordinate plane, getting this.

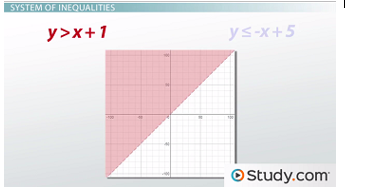
We could then graph the second inequality, y = -x + 5 directly on top of it to get this.

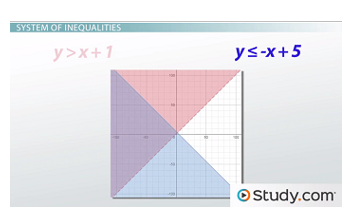
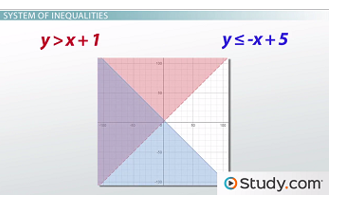
Since we want to know where both inequalities are true, we're looking for the area where the shading overlaps, leaving our answer as the purple area in this graph.

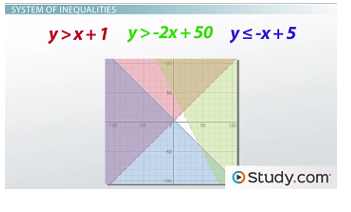
There are times when a system of inequalities will not have a solution. Let's expand our previous example by adding a third inequality: y > -2x + 50. We want to know if there is a set of solutions for which all three inequalities are true. As we can see from the graph, there are several places where the shading for any two of the three inequalities overlaps, but no single area where all three overlap. That means that there is no solution to this set of three inequalities, which is a perfectly valid answer!

Lesson Summary

To review, compound inequalities are problems with two 1-variable inequalities in them. If an answer must satisfy both inequalities, it is called an 'and' compound inequality, but if satisfying one of the inequalities is enough to be a solution, then it is called an 'or' compound inequality. There are two mathematical notations commonly used to describe the solution sets of compound inequalities: set notation and interval notation.

Systems of inequalities are problems with two or more 2-variable inequalities. You can graph a system of inequalities by working with one inequality at a time.