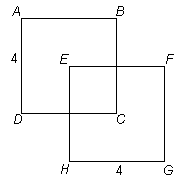
What is the area of the region in which squares ABCD
and EFGH overlap?
1) F bisects BC
2) 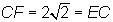
- What do we know about the two figures and the overlapping
area?
- What are we unable to determine about the two figures
and the overlapping area?
1) EF bisects BC
| |

|
Sufficient |
 |
Insufficient |
|
|
2) 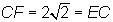
| |

|
Sufficient |

|
Insufficient |
|
|
Countinue
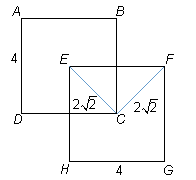
This tells us that a line segment drawn between C and F
and a line segment drawn between C and E both have a length
of 2v. What can we do
with this? First, seeing v
in a question involving squares should immediately make you think of isosceles
right triangles, since a square cut along its diagonal yields two isosceles
right triangles, which we know have side lengths in the ratio of x:x:
xv. Knowing this,
you should actually draw the diagram on your scrap paper and pencil in
these two line segments. You’d get something that looks like the modified
diagram above.
We know from Statement 2 that the distance from C to F
and from C to E is 2v,
but what we don’t know is the orientation of square EFGH in relation
to square ABCD. In other words, square EFGH doesn’t necessarily
have to be oriented so that its sides are perfectly vertical and horizontal.
It could look like this, for example:
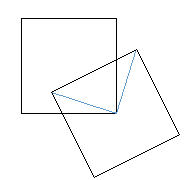
Without knowing the
orientation of square EFGH, we can’t figure out any of the side
lengths of the overlapping portion of the two squares. So Statement (2)
is also insufficient.
Now, let’s try looking at the two statements together:
Countinue
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ