Lesson: Chapter - 7

Explanations

1.      C     

When the force is exerted in the direction of motion, work is simply the product of force and displacement. The work done is (10 N)(4.0 m) = 40 J.

2.      D     

The work done on the box is the force exerted multiplied by the box’s displacement. Since the box travels at a constant velocity, we know that the net force acting on the box is zero. That means that the force of the person’s push is equal and opposite to the force of friction. The force of friction is given by µN, where µ is the coefficient of kinetic friction and N is the normal force. The normal force is equal to the weight of the box, which is mg = (10 kg )(10 m/s²) = 100 N. With all this in mind, we can solve for the work done on the box:

W = µN(4m) = (0.3)(100N)(4m) = 120J

3.      C     

The work done by the force of gravity is the dot product of the displacement of the box and the force of gravity acting on the box. That means that we need to calculate the component of the force of gravity that is parallel to the incline. This is mg sin 30 = (10 kg)(10 m/s²) sin 30. Thus, the work done is

W = mg sin 30(8.0m) = (10kg)(10m/s²)(0.5)(8.0m) = 400J

4.      C     

This is the same question as question 1. We were hoping that with different numbers and line spacing you wouldn’t notice. The test writers do that too sometimes.

5.      C     

On a force vs. displacement graph, the amount of work done is the area between the graph and the x-axis. The work Al does is the area of the 4 × &minus 4 right triangle:

1/2 (-4N)(4m) = -8J

The amount of work Betty does is equal to the area of a triangle of length 2 and height 4:

1/2(4N)(2m) = 4J

The amount of work done by Chuck is equal to the area of a rectangle of length 2 and height 4: 4 × 2 = 8 J. We can conclude that Chuck did the most work.

Don’t be fooled by D: the force exerted by Al is in the opposite direction of the object’s displacement, so he does negative work on the object.

6.      E     

The formula for kinetic energy is KE = 1/2 mv². Since the car’s kinetic energy is directly proportional to the square of its velocity, doubling the velocity would mean quadrupling its kinetic energy.

7.      A     

The work-energy theorem tells us that the amount of work done on an object is equal to the amount of kinetic energy it gains, and the amount of work done by an object is equal to the amount of kinetic energy it loses. The box gains 500 J of kinetic energy from the worker’s push, and loses 375 J of kinetic energy to friction, for a net gain of 125 J. Kinetic energy is related to velocity by the formula KE = 1/2 mv², so we can get the answer by plugging numbers into this formula and solving for v:

8.      C     

When the book reaches the person in the window, it will have a gravitational potential energy of U = mgh. In order for the book to reach the window, then, it must leave the hands of the person at street level with at least that much kinetic energy. Kinetic energy is given by the formula KE = ¹/₂ mv², so we can solve for v by making KE U :

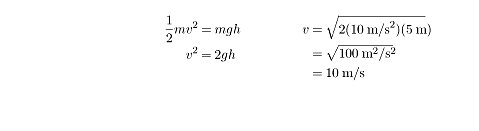
9.      B     

Power is a measure of work divided by time. In turn, work is a measure of force multiplied by displacement. Since the crate is lifted with a constant velocity, we know that the net force acting on it is zero, and so the force exerted by the forklift must be equal and opposite to the weight of the crate, which is (100 kg)(10 m/s²) = 1.0 × 10³ N. From this, we can calculate the power exerted by the forklift:

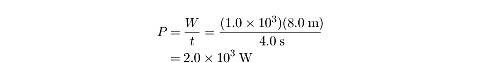
10.      A     

Power is measured as work divided by time, and work is the dot product of force and displacement. While the crate is being held in the air, it is not displaced, so the displacement is zero. That means the forklift does no work, and thus exerts no power.

Next to display next topic in the chapter.