Geometry - Angles

• Angle - A figure formed by two lines sharing a common endpoint.
• Ray - A straight line extending from a point.
• Acute Angle - An angle less than 90° and greater than 0°
• Obtuse Angle - An angle between 90° and 180°
• Right Angle - An angle that is exactly 90°
• Complementary Angles - Two angles whose sum is 90°
• Supplementary Angles - Two angles whose sum is 180°
• Adjacent Angles - Two angles that share a side (i.e., are adjacent).
• Angle Bisector - A ray that divides an angle into two equal parts.
• Vertical Angles - The two non-adjacent angles that share a vertex when two lines intersect.
• Alternate Interior Angles - When two parallel lines are cut by a transversal, the two angles on opposite sides of the transversal and between the parallel lines.
• Alternate Exterior Angles - When two parallel lines are cut by a transversal, the two angles on opposite sides of the transversal and outside the parallel lines.

Types of Angles

Acute Angle

An acute angle is one whose measurement is less than 90°. Angle A, shown below, is an acute angle.

Obtuse Angle

An obtuse angle is one whose measurement is greater than 90° and less than 180°. Angle B, shown below, is an obtuse angle.

Right Angle

A right angle is one whose measurement is exactly 90°. Angle C, shown below, is a right angle.

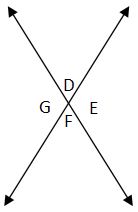
Intersecting Lines

When two lines intersect, they form four angles. Angles that are not adjacent (i.e., do not share a common side) are called vertical angles and these angles are congruent (or equal in measurement).

Due to the properties of intersecting lines, vertical angles are congruent. Consequently, angle D = angle F and angle G = angle E.

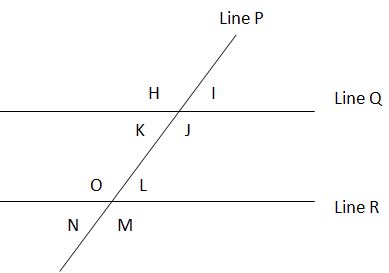
Parallel Lines Cut by a Transversal

When two parallel lines are cut by a transversal (i.e., a third line intersects the two parallel lines), a number of relationships exist between the resulting angles.

Alternate Interior Angles Are Equal: K = L; O = J

Alternate Exterior Angles Are Equal: H = M; N = I

Corresponding Angles Are Equal: K = N; J = M; H = O; I = L

Non-Alternate Interior Angles Are Supplementary: L + J = 180; K + O = 180

It is important to note that if two lines cut by a transversal have any of the above properties, then the two lines must be parallel. For example, if alternate interior angles are equal, then the two lines cut by a transversal must be parallel.

Sum of Angles

The sum of the interior angles of a polygon is 180 × (n - 2) where n is the number of sides. For example, the sum of the interior angles of a triangle is 180 = (180)(3 - 2) while the sum of the interior angles of a square is 360 = (180)(4 - 2).