Square Root And Cube Root

How to find the square root of 4 digit number?

• Step 1: Ignore last two digits 24 and just consider first three digits.
• Step 2: Find a number near or less than 60.49 is a number near to 60 which is perfect square of 7. Hence, the number in ten’s place is 7.
• Step 3: Find the number in unit’s place: 4 is the number in unit’s place. Hence, remember the table, 2 and 8 numbers have unit’s digit 4.
• Step 4: Now we have to find the correct number among 2 and 8.
• Step 5: Multiply 7 with next higher number (7+1) = 8 i .e 7×8 = 56. Number 56 is less than the first two digits, hence consider the largest number among 2 and 8 i.e 8. Therefore, second number is 8.
  Square root of 6084 = 78

How to find the square root of 3 digit number?

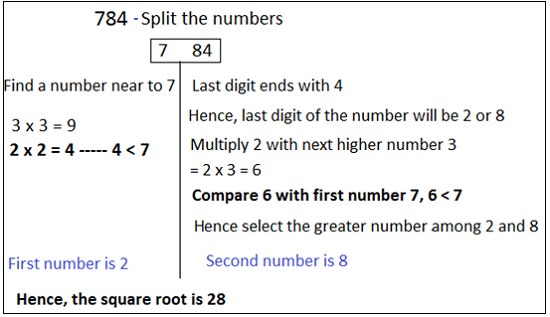
• Step 1: Ignore last two digits 24 and just consider first three digits.
• Step 2: Find a number near or less than 7.4 is a number near to 7 which is perfect square of 2. Hence, the number in ten’s place is 2.
• Step 3: Find the number in unit’s place: 4 is the number in unit’s place. Hence, remember the table, 2 and 8 numbers have unit’s digit 4.
• Step 4: Now we have to find the correct number among 2 and 8.
• Step 5: Multiply 7 with next higher number (2+1 = 8) i .e 2×3 = 6. Number 6 is less than the first digits, hence consider the largest number among 2 and 8 i.e 8. Therefore, second number is 8.
  Square root of 784 = 28

2) Finding the square of large numbers

Example: 47² = 2209
Square of 47 can be easily determined by following the steps shown below:
Step 1: Split the number 47 as 4 and 7.
Step 2: Use the formula: (a + b)² = a² + 2ab + b²
Here, (4 + 7)² = 4² + 2 × 4 × 7 + 7²
Without considering the plus sign, write the numbers as shown below:
[16] [56] [49]

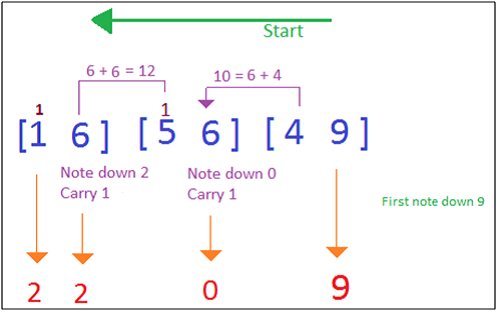
• Step 1: Write down 9 from 49 and carry 4 to 56. [-----9]
• Step 2: After adding 4 to 6, we get 10. Therefore, write down zero and carry 1 (5 + 1 = 6) to 16. [----09]
• Step 3: 6 + 6 = 12, write down 2 and carry one. [---209]
• Step 4: Finally write the answer along with (1 + 1 = 2). [2209]

3) Finding the cube root of 6 digit number?

Note: Cube roots of 6, 5, 4 or 3 digit numbers can be easily found out by using the same trick as used to find the square root of larger digits.
Example: 3√132651
Remember: The last 3 numbers are to cut off and the nearby cube of first remaining numbers is to be found out.

• Step 1: Split the number 132 and 651
• Step 2: 125 is the cube of 5, which is the closest number to 132. Hence, first number i.e. the number in ten’s place is 5.
• Step 3: 1 is the digit in unit’s place. Hence, the digit in unit’s place is 1.
  Hence, the cube root of 132651 is 51.

4) How to find a number to be added or subtracted to make a number a perfect square ?

For easy understanding, let’s take an example. Example: 8888



• Step 1: Divide 8888 by 9. We get remainder 7.
• Step 2: Add Divisor and Quotient [9 + 9 = 18]
• Step 3: Now the next divisor will be (18 and number x) which will divide the next dividend. In this case, 4 is the number x and now the divisor becomes 184 × 4 =736.
• Step 1: This step is to be followed depend the number of digits in the dividend.

Case 1: If we have to find a number to be added to make a number perfect square, then Consider a number greater than the quotient. Her quotient is 94, hence consider 95.
94² < 8888 < 95²
8836 < 8888 < 9025
Number to be added = Greater number – Given number
Number to be added = 9025 – 8888 = 137

Case 2: If we have to find a number to be subtracted to make a number perfect square, then
94² < 8888 < 95²
8836 < 8888 < 9025
Number to be subtracted = Given number - Smaller number
Number to be added = 8888 – 8836 = 52