Lesson: Chapter - 9

Conservation of Momentum

If we combine Newton’s Third Law with what we know about impulse, we can derive the important and extremely useful law of conservation of momentum.

Newton’s Third Law tells us that, to every action, there is an equal and opposite reaction. If object A exerts a force F on object B, then object B exerts a force –F on object A. The net force exerted between objects A and B is zero.

The impulse equation, J = F?t = ?p, tells us that if the net force acting on a system is zero, then the impulse, and hence the change in momentum, is zero. Because the net force between the objects A and B that we discussed above is zero, the momentum of the system consisting of objects A and B does not change.

Suppose object A is a cue ball and object B is an eight ball on a pool table. If the cue ball strikes the eight ball, the cue ball exerts a force on the eight ball that sends it rolling toward the pocket. At the same time, the eight ball exerts an equal and opposite force on the cue ball that brings it to a stop. Note that both the cue ball and the eight ball each experience a change in momentum. However, the sum of the momentum of the cue ball and the momentum of the eight ball remains constant throughout. While the initial momentum of the cue ball, P_A, is not the same as its final momentum, P_Á, and the initial momentum of the eight ball, P_B, is not the same as its final momentum, P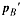, the initial momentum of the two balls combined is equal to the final momentum of the two balls combined:

The conservation of momentum only applies to systems that have no external forces acting upon them. We call such a system a closed or isolated system: objects within the system may exert forces on other objects within the system (e.g., the cue ball can exert a force on the eight ball and vice versa), but no force can be exerted between an object outside the system and an object within the system. As a result, conservation of momentum does not apply to systems where friction is a factor.

Conservation of Momentum on subject test Physics

The conservation of momentum may be tested both quantitatively and qualitatively on subject test Physics. It is quite possible, for instance, that subject test Physics will contain a question or two that involves a calculation based on the law of conservation of momentum. In such a question, “conservation of momentum” will not be mentioned explicitly, and even “momentum” might not be mentioned. Most likely, you will be asked to calculate the velocity of a moving object after a collision of some sort, a calculation that demands that you apply the law of conservation of momentum.

Alternately, you may be asked a question that simply demands that you identify the law of conservation of momentum and know how it is applied. The first example we will look at is of this qualitative type, and the second example is of a quantitative conservation of momentum question.

Example 1

Although the title of the section probably gave the solution away, we phrase the problem in this way because you’ll find questions of this sort quite a lot on subject test Physics. You can tell a question will rely on the law of conservation of momentum for its solution if you are given the initial velocity of an object and are asked to determine its final velocity after a change in mass or a collision with another object.

Some Supplemental Calculations

But how would we use conservation of momentum to find the speed of the toy truck after the apple has landed?

First, note that the net force acting in the x direction upon the apple and the toy truck is zero. Consequently, linear momentum in the x direction is conserved. The initial momentum of the system in the x direction is the momentum of the toy truck,P_i = Mv.

Once the apple is in the truck, both the apple and the truck are traveling at the same speed, V_f. Therefore, V_f = mv_f + Mv_f = (m + M)v_f. Equating P_i and P_f, we find:

As we might expect, the final velocity of the toy truck is less than its initial velocity. As the toy truck gains the apple as cargo, its mass increases and it slows down. Because momentum is conserved and is directly proportional to mass and velocity, any increase in mass must be accompanied by a corresponding decrease in velocity.

Example 2

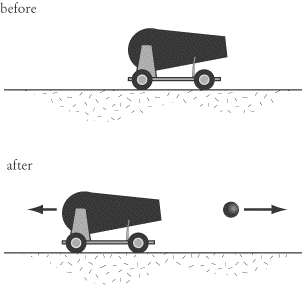
A cannon of mass 1000 kg launches a cannonball of mass 10 kg at a velocity of 100 m/s. At what speed does the cannon recoil?

Questions involving firearms recoil are a common way in which subject test Physics may test your knowledge of conservation of momentum. Before we dive into the math, let’s get a clear picture of what’s going on here. Initially the cannon and cannonball are at rest, so the total momentum of the system is zero. No external forces act on the system in the horizontal direction, so the system’s linear momentum in this direction is constant. Therefore the momentum of the system both before and after the cannon fires must be zero.

Now let’s make some calculations. When the cannon is fired, the cannonball shoots forward with momentum (10 kg)(100 m/s) = 1000 kg · m/s. To keep the total momentum of the system at zero, the cannon must then recoil with an equal momentum:

P_cannon = mv_cannon

= 1000 kg.ms = (1000 kg)v_cannon

v_cannon = 1 m/s

Any time a gun, cannon, or an artillery piece releases a projectile, it experiences a “kick” and moves in the opposite direction of the projectile. The more massive the firearm, the slower it moves.

Next to display next topic in the chapter.