Work When Force and Displacement Are Parallel
When the force exerted on an object is in the same direction as the displacement
of the object, calculating work is a simple matter of multiplication. Suppose
you exert a force of 10 N on a box in the
northward direction, and the box moves 5 m
to the north. The work you have done on the box is
10 N × 5 m = 50 N.m = 50 J. If force and displacement are
parallel to one another, then the work done by a force is simply the product of
the magnitude of the force and the magnitude of the displacement.
Work When Force and Displacement Are Not Parallel
Unfortunately, matters aren’t quite as simple as scalar multiplication when the
force and displacement vectors aren’t parallel. In such a case, we define work
as the product of the displacement of a body and the component of the force in
the direction of that displacement. For instance, suppose you push a box with a
force F along the floor for a
distance s, but rather than
pushing it directly forward, you push on it at a downward angle of
45°. The work you do on the box is not
equal to
F × s,
the magnitude of the force times the magnitude of the displacement. Rather, it
is equal to
Fs × s,
the magnitude of the force exerted in the direction of the displacement times
the magnitude of the displacement.

Some simple trigonometry shows us that Fs = F cos? , where ? is the angle between the F vector
and the s vector. With this in mind, we can express a general formula for the work
done by a force, which applies to all cases:
W = Fs × s = Fs cos?
This formula also applies to the cases where F and s are parallel,
since in those cases, ? = 0 , and cos ? = 1 , so W = Fs.
Dot Product
What the formula above amounts to is that work is the dot product of
the force vector and the displacement vector. As we recall, the dot product
of two vectors is the product of the magnitudes of the two vectors multiplied
by the cosine of the angle between the two vectors. So the most general vector
definition of work is:
W = F.s = Fs cos ?
Review
The concept of work is actually quite straightforward, as you’ll see with a
little practice. You just need to bear a few simple points in mind:
- If force and displacement are both in the same direction, the work done is the
product of the magnitudes of force and displacement.
- If force and displacement are at an angle to one another, you need to calculate
the component of the force that points in the direction of the displacement, or
the component of the displacement that points in the direction of the force. The
work done is the product of the one vector and the component of the other
vector.
- If force and displacement are perpendicular, no work is done.
Because of the way work is defined in physics, there are a number of cases that
go against our everyday intuition. Work is not done whenever a force is exerted,
and there are certain cases in which we might think that a great deal of work is
being done, but in fact no work is done at all. Let’s look at some examples that
might be tested on subject test Physics:
- You do work on a 10 kg mass when you lift
it off the ground, but you do no work to hold the same mass stationary in the
air. As you strain to hold the mass in the air, you are actually making sure
that it is not displaced. Consequently, the work you do to hold it is zero.
- Displacement is a vector quantity that is not the same thing as distance
traveled. For instance, if a weightlifter raises a dumbbell 1 m, then lowers it
to its original position, the weightlifter has not done any work on the dumbell.
- When a force is perpendicular to the direction of an object’s motion, this force
does no work on the object. For example, say you swing a tethered ball in a
circle overhead, as in the diagram below. The tension force,
T, is always perpendicular to
the velocity, v, of the ball,
and so the rope does no work on the ball.

Example

A water balloon of mass m is dropped from a height h. What is the work
done on the balloon by gravity? How much work is done by gravity if the
balloon is thrown horizontally from a height h with an initial velocity of V0 ?
What is the work done on the balloon by gravity?
Since the gravitational force of –mg
is in the same direction as the water balloon’s displacement,
–h, the work done by the
gravitational force on the ball is the force times the displacement, or
W = mgh, where
g = –9.8 m/s2.
How much work is done by gravity if the balloon is thrown horizontally from a
height h with an initial velocity of v0?
The gravitational force exerted on the balloon is still
–mg, but the displacement is
different. The balloon has a displacement of –h
in the y direction and d
(see the figure below) in the x direction. But, as we recall, the
work done on the balloon by gravity is not simply the product of the magnitudes
of the force and the displacement. We have to multiply the force by the
component of the displacement that is parallel to the force. The force is
directed downward, and the component of the displacement that is directed
downward is –h. As a result, we find
that the work done by gravity is mgh,
just as before.
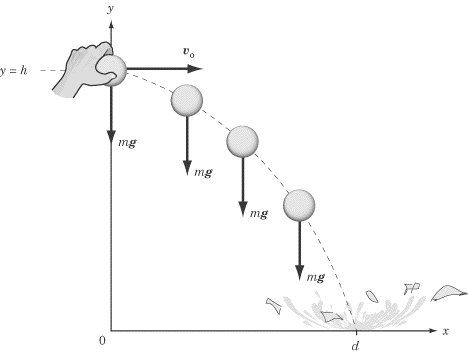
The work done by the force of gravity is the same if the object falls
straight down or if it makes a wide parabola and lands 100 m to the east.
This is because the force of gravity does no work when an object is transported
horizontally, because the force of gravity is perpendicular to the horizontal
component of displacement.
Work Problems with Graphs
There’s a good chance subject test Physics may test your understanding of work
by asking you to interpret a graph. This graph will most likely be a force vs.
position graph, though there’s a chance it may be a graph of Fcos? vs. position. Don’t
let the appearance of trigonometry scare you: the principle of reading graphs
is the same in both cases. In the latter case, you’ll be dealing with a graphic
representation of a force that isn’t acting parallel to the displacement, but the
graph will have already taken this into account. Bottom line: all graphs dealing
with work will operate according to the same easy principles.
The most important thing that you need to remember about these graphs is:
The work done in a force vs. displacement graph is equal to the area
between the graph and the x-axis during the same interval.
If you recall your kinematics graphs, this is exactly what you would do to
read velocity on an acceleration vs. time graph, or displacement on a velocity vs.
time graph. In fact, whenever you want a quantity that is the product of the quantity
measured by the y-axis and the quantity measured by the x-axis, you can simply calculate
the area between the graph and the x-axis.
Example

The graph above plots the force exerted on a box against the displacement of the box.
What is the work done by the force in moving the box from x = 2 to x = 4?
The work done on the box is equal to the area of the shaded region in the figure above,
or the area of a rectangle of width 2 and height 4 plus the area of a right triangle of base 2
and height 2. Determining the amount of work done is simply a matter of calculating the area of
the rectangle and the area of the triangle, and adding these two areas together:
2.4 +1/2.2.2 = 10J
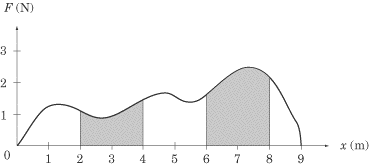
Curved Force vs. Position Graphs
If subject test Physics throws you a curved force vs. position graph, don’t panic. You
won’t be asked to calculate the work done, because you can’t do that without
using calculus. Most likely, you’ll be asked to estimate the area beneath the
curve for two intervals, and to select the interval in which the most, or least,
work was done. In the figure below, more work was done between
x = 6 and
x = 8 than between
x = 2 and x = 4, because the area between the
graph and the x-axis is larger for the interval between
x = 6 and
x = 8.
Back
Next
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.