Lesson: Chapter - 6

Types of Forces

There are a number of forces that act in a wide variety of cases and have been given specific names. Some of these, like friction and the normal force, are so common that we’re hardly aware of them as distinctive forces. It’s important that you understand how and when these forces function, because questions on SAT II Physics often make no mention of them explicitly, but expect you to factor them into your calculations. Some of these forces will also play an important role in the chapter on special problems in mechanics.

Weight

Although the words weight and mass are often interchangeable in everyday language, these words refer to two different quantities in physics. The mass of an object is a property of the object itself, which reflects its resistance to being accelerated. The weight of an object is a measure of the gravitational force being exerted upon it, and so it varies depending on the gravitational force acting on the object. Mass is a scalar quantity measured in kilograms, while weight is a vector quantity measuring force, and is represented in newtons. Although an object’s mass never changes, its weight depends on the force of gravity in the object’s environment.

For example, a 10 kg mass has a different weight on the moon than it does on Earth. According to Newton’s Second Law, the weight of a 10 kg mass on Earth is

F = mg_earth

= (10kg)(9.8m/s²⁾

= 98N

This force is directed toward the center of the Earth. On the moon, the acceleration due to gravity is roughly one-sixth that on Earth. Therefore, the weight of a 10 kg mass on the moon is only about 16.3 N toward the center of the moon.

The Normal Force

The normal force always acts perpendicular (or “normal”) to the surface of contact between two objects. The normal force is a direct consequence of Newton’s Third Law. Consider the example of a 10 kg box resting on the floor. The force of gravity causes the box to push down upon the ground with a force, W, equal to the box’s weight. Newton’s Third Law dictates that the floor must apply an equal and opposite force, N = –W, to the box. As a result, the net force on the box is zero, and, as we would expect, the box remains at rest. If there were no normal force pushing the box upward, there would be a net force acting downward on the box, and the box would accelerate downward

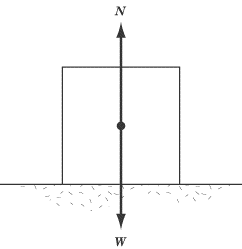
Be careful not to confuse the normal force vector N with the abbreviation for newtons, N. It can be a bit confusing that both are denoted by the same letter of the alphabet, but they are two totally different entities.

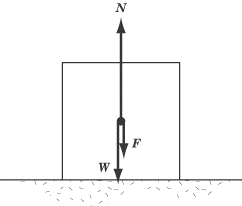
Example

A person pushes downward on a box of weight W with a force F. What is the normal force, N, acting on the box?

The total force pushing the box toward the ground is W + F. From Newton’s Third Law, the normal force exerted on the box by the floor has the same magnitude as W + F but is directed upward. Therefore, the net force on the box is zero and the box remains at rest.

Friction

Newton’s First Law tells us that objects in motion stay in motion unless a force is acting upon them, but experience tells us that when we slide coins across a table, or push boxes along the floor, they slow down and come to a stop. This is not evidence that Newton was wrong; rather, it shows that there is a force acting upon the coin or the box to slow its motion. This is the force of friction, which is at work in every medium but a vacuum, and is the bugbear of students pushing boxes across the sticky floors of dorm rooms everywhere.

Roughly speaking, frictional forces are caused by the roughness of the materials in contact, deformations in the materials, and molecular attraction between materials. You needn’t worry too much over the causes of friction, though: SAT II Physics isn’t going to test you on them. The most important thing to remember about frictional forces is that they are always parallel to the plane of contact between two surfaces, and opposite to the direction that the object is being pushed or pulled.

There are two main types of friction: static friction and kinetic friction. Kinetic friction is the force between two surfaces moving relative to one another, whereas static friction is the force between two surfaces that are not moving relative to one another.

Static Friction

Imagine, once more, that you are pushing a box along a floor. When the box is at rest, it takes some effort to get it to start moving at all. That’s because the force of static friction is resisting your push and holding the box in place.

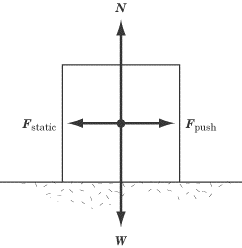
In the diagram above, the weight and the normal force are represented as W and N respectively, and the force applied to the box is denoted by F_push. The force of static friction is represented by F_static, where F_static = F_push. The net force on the box is zero, and so the box does not move. This is what happens when you are pushing on the box, but not hard enough to make it budge.

Static friction is only at work when the net force on an object is zero, and hence when F_static = -F_push. If there is a net force on the object, then that object will be in motion, and kinetic rather than static friction will oppose its motion.

Kinetic Friction

The force of static friction will only oppose a push up to a point. Once you exert a strong enough force, the box will begin to move. However, you still have to keep pushing with a strong, steady force to keep it moving along, and the box will quickly slide to a stop if you quit pushing. That’s because the force of kinetic friction is pushing in the opposite direction of the motion of the box, trying to bring it to rest.

Though the force of kinetic friction will always act in the opposite direction of the force of the push, it need not be equal in magnitude to the force of the push. In the diagram above, the magnitude of F_kinetic is less than the magnitude of F_push. That means that the box has a net force in the direction of the push, and the box accelerates forward. The box is moving at velocity v in the diagram, and will speed up if the same force is steadily applied to it. If F_push were equal to -F_kinetic, the net force acting on the box would be zero, and the box would move at a steady velocity of v, since Newton’s First Law tells us that an object in motion will remain in motion if there is no net force acting on it. If the magnitude of F_push were less than the magnitude of F_kinetic, the net force would be acting against the motion, and the box would slow down until it came to a rest.

The Coefficients of Friction

The amount of force needed to overcome the force of static friction on an object, and the magnitude of the force of kinetic friction on an object, are both proportional to the normal force acting on the object in question. We can express this proportionality mathematically as follows:

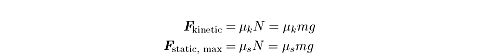
where U_k is the coefficient of kinetic friction, U_k is the coefficient of static friction, and N is the magnitude of the normal force. The coefficients of kinetic and static friction are constants of proportionality that vary from object to object.

Note that the equation for static friction is for the maximum value of the static friction. This is because the force of static friction is never greater than the force pushing on an object. If a box has a mass of 10 kg and U₅ = 0.5, then:

F_{static, max} = 0.5(10kg)<9.8m/s²⁾

= 49 N

If you push this box with a force less than 49 newtons, the box will not move, and consequently the net force on the box must be zero. If an applied force is less F_push thanF_static,max , then F_static = –F_push.

Three Reminders

Whenever you need to calculate a frictional force on subject test Physics, you will be told the value of µ , which will fall between 0 and 1. Three things are worth noting about frictional forces:

1. The smaller µ is, the more slippery the surface. For instance, ice will have much lower coefficients of friction than Velcro. In cases where µ , the force of friction is zero, which is the case on ideal frictionless surfaces.
2. The coefficient of kinetic friction is smaller than the coefficient of static friction. That means it takes more force to start a stationary object moving than to keep it in motion. The reverse would be illogical: imagine if you could push on an object with a force greater than the maximum force of static friction but less than the force of kinetic friction. That would mean you could push it hard enough to get it to start moving, but as soon as it starts moving, the force of kinetic friction would push it backward.
3. Frictional forces are directly proportional to the normal force. That’s why it’s harder to slide a heavy object along the floor than a light one. A light coin can slide several meters across a table because the kinetic friction, proportional to the normal force, is quite small.

Example

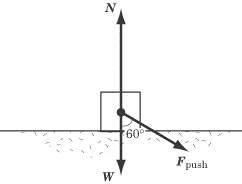
A student pushes a box that weighs 15 N with a force of 10 N at a 60Šangle to the perpendicular. The maximum coefficient of static friction between the box and the floor is 0.4. Does the box move? Note that sin 60º = 0.866 and cos 60Š= 0.500.

In order to solve this problem, we have to determine whether the horizontal component of F_push is of greater magnitude than the maximum force of static friction.

We can break the F_push vector into horizontal and vertical components. The vertical component will push the box harder into the floor, increasing the normal force, while the horizontal component will push against the force of static friction. First, let’s calculate the vertical component of the force so that we can determine the normal force, N, of the box:

F_{push y} = F_push cos60° = 0.500 (10N) = 5.0 N

If we add this force to the weight of the box, we find that the normal force is 15 + 5.0 = 20 N. Thus, the maximum force of static friction is:

F_static,max = µN = 4.0(20N) = 8.0N

The force pushing the box forward is the horizontal component of F_push , which is:

F_{push x} = F_pushsin60° = 0.866(10N) = 8.66N

As we can see, this force is just slightly greater than the maximum force of static friction opposing the push, so the box will slide forward.

Tension

Consider a box being pulled by a rope. The person pulling one end of the rope is not in contact with the box, yet we know from experience that the box will move in the direction that the rope is pulled. This occurs because the force the person exerts on the rope is transmitted to the box.

The force exerted on the box from the rope is called the tension force, and comes into play whenever a force is transmitted across a rope or a cable. The free-body diagram below shows us a box being pulled by a rope, where W is the weight of the box, N is the normal force, T is the tension force, and F_f is the frictional force.

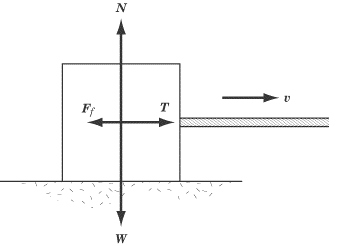
In cases like the diagram above, it’s very easy to deal with the force of tension by treating the situation just as if there were somebody behind the box pushing on it. We’ll find the force of tension coming up quite a bit in the chapter on special problems in mechanics, particularly when we deal with pulleys.

Next to display next topic in the chapter.