Lesson: Chapter - 17
The Doppler Effect
So far we have only discussed cases where the source of waves is at rest. Often,
waves are emitted by a source that moves with respect to the medium that carries
the waves, like when a speeding cop car blares its siren to alert onlookers to
stand aside. The speed of the waves, v,
depends only on the properties of the medium, like air temperature in the case
of sound waves, and not on the motion of the source: the waves will travel at
the speed of sound (343 m/s) no matter how
fast the cop drives. However, the frequency and wavelength of the waves will
depend on the motion of the wave’s source.
This change in frequency is
called a Doppler shift.Think of the cop car’s siren, traveling at speed
vs,
and emitting waves with frequency f
and period T =
1/f.
The wave crests travel outward from the car in perfect circles (spheres
actually, but we’re only interested in the effects at ground level). At time
T after the first wave crest is
emitted, the next one leaves the siren. By this time, the first crest has
advanced one wavelength,
?,
but the car has also traveled a distance of
vsT.
As a result, the two wave crests are closer together than if the cop car had
been stationary.
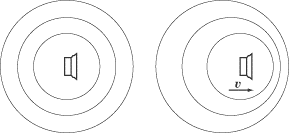
The shorter wavelength is called the Doppler-shifted wavelength, given by the
formula
?D = ? - vsT = ?(v - vs) / v.
The Doppler-shifted frequency is given by the formula:
ƒD = ƒ v/v - vs
Similarly, someone standing behind the speeding siren will hear a sound with a
longer wavelength,
?D = ? + vsT = ?(v + vs)v ,
and a lower frequency,
ƒD = ƒ v/ (v + vs).
You’ve probably noticed the Doppler effect with passing sirens. It’s even
noticeable with normal cars: the swish of a passing car goes from a higher
hissing sound to a lower hissing sound as it speeds by. The Doppler effect has
also been put to valuable use in astronomy, measuring the speed with which
different celestial objects are moving away from the Earth.
Example
A cop car drives at 30 m/s toward the scene of a crime, with its siren blaring
at a frequency of 2000 Hz. At what frequency do people hear the siren as it
approaches? At what frequency do they hear it as it passes? The speed of sound
in the air is 343 m/s.
As the car approaches, the sound waves will have shorter wavelengths and higher
frequencies, and as it goes by, the sound waves will have longer wavelengths and
lower frequencies. More precisely, the frequency as the cop car approaches is:
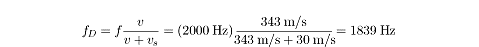
The frequency as the cop car drives by is:
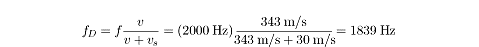
Back
Next
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.