Lesson: Chapter - 15

Magnetic Force on Current-Carrying Wires

Since an electric current is just a bunch of moving charges, wires carrying current will be subject to a force when in a magnetic field. When dealing with a current in a wire, we obviously can’t use units of q and v. However, qv can equally be expressed in terms of Il, where I is the current in a wire, and l is the length, in meters, of the wire—both qv and Il are expressed in units of C · m/s. So we can reformulate the equation for the magnitude of a magnetic force in order to apply it to a current-carrying wire:

Video Lesson

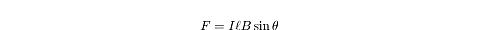
In this formulation, ? is the angle the wire makes with the magnetic field. We determine the direction of the force by using the right-hand rule between the direction of the current and that of the magnetic field.

Example

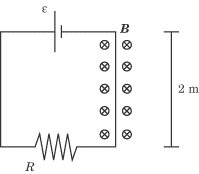
In the figure above, a magnetic field of 4.0 × 10^-5 T is applied locally to one part of an electric circuit with a 5 O resistor and a voltage of 30 V. The length of wire to which the magnetic field is applied is 2 m. What is the magnetic force acting on that stretch of wire?

We are only interested in the stretch of wire on the right, where the current flows in a downward direction. The direction of current is perpendicular to the magnetic field, which is directed into the page, so we know the magnetic force will have a magnitude of F = IlB, and will be directed to the right.

We have been told the magnetic field strength and the length of the wire, but we need to calculate the current in the wire. We know the circuit has a voltage of 30 V and a resistance of 5 O, so calculating the current is just a matter of applying Ohm’s Law:

Now that we know the current, we can simply plug numbers into the equation for the force of a magnetic field on a current-carrying wire:

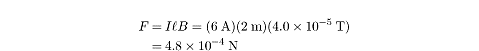
Next to display next topic in the chapter.