Lesson: Chapter - 14
Capacitors
Capacitors rarely come up on Physics, but they do sometimes make
an appearance. Because capacitance is the most complicated thing you need to
know about DC circuits, questions on capacitors will usually reward you simply
for knowing what’s going on. So long as you understand the basic principles at
work here, you’re likely to get a right answer on a question most students will
answer wrong.
Video Lesson - Capacitor
A capacitor is a device for storing charge, made up of two parallel plates with
a space between them. The plates have an equal and opposite charge on them,
creating a potential difference between the plates. A capacitor can be made of
conductors of any shape, but the parallel-plate capacitor is the most
common kind. In circuit diagrams, a capacitor is represented by two equal
parallel lines.

For any capacitor, the ratio of the charge to the potential difference is called
the capacitance, C:
C = Q/?V
For a parallel-plate capacitor, C is
directly proportional to the area of the plates,
A, and inversely proportional to the distance between them,
d. That is, if the area of the
plates is doubled, the capacitance is doubled, and if the distance between the
plates is doubled, the capacitance is halved. The proportionality constant
between C and
A/d is
e0,
called the permittivity of free space, which we encountered in the previous
chapter in relation to Coulomb’s constant. In case you forgot,
e0 = 8.85 × 10-10
C2 /N · m2.
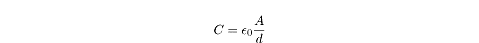
The unit of capacitance is the farad (F). One farad is equal to one
coulomb per volt. Most capacitors have very small capacitances, which are
usually given in microfarads, where 1 µF =
10–6 F.
Energy
To move a small amount of negative charge from the positive plate to the
negative plate of a capacitor, an external agent must do work. This work is the
origin of the energy stored by the capacitor.
If the plates have a charge of magnitude q,
the potential difference is
?V = q/C.
If q = 0, and work is done to add
charge until q = Q, the total work
required is:
U = 1/2 Q?V
This is the energy stored by the capacitor. Manipulating this equation and the
equation for capacitance,
C = Q/?V ,
we can derive a number of equivalent forms:
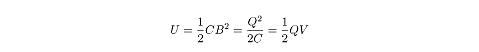
Equivalent Capacitance
Like resistors, capacitors can be arranged in series or in parallel. The rule
for adding capacitance is the reverse of adding resistance:
Capacitors in series add like resistors in parallel, and capacitors in parallel
add like resistors in series.
For two capacitors in series:

For two capacitors in parallel:
Ct = C1 + C2
Video Lesson - Capacitor in Series and Parallel Circuits
Example
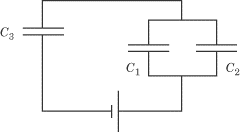
|
|
|
|
|
Given
C1
= 2 µF,
C2
= 6 µF, and
C3
= 3 µF, what is the total capacitance of the circuit in the figure above?
|
First, we find the equivalent capacitance of
C1
and
C2.
Since they are in parallel,
C1+2
=
C1
+
C2
= 8 µF. Then
Ct
is given by:

Dielectricss
One way to keep the plates of a capacitor apart is to insert an insulator called
a dielectric between them. A dielectric increases the capacitance. There
is an electric field between the plates of a capacitor. This field polarizes the
molecules in the dielectric; that is, some of the electrons in the molecules
move to the end of the molecule, near the positive plate:
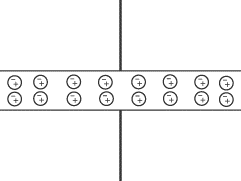
The movement of electrons creates a layer of negative charge by the positive
plate and a layer of positive charge by the negative plate. This separation of
charge, in turn, creates an electric field in the dielectric that is in the
opposite direction of the original field of the capacitor. This reduces the
total electric field:
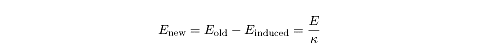
The Greek letter
k
is called the dielectric constant, and it varies from material to
material. For all materials,
k
> 1.
For a parallel-plate capacitor, the reduction in
E means that
?V
is also reduced by a factor of
k.
Then, since C = Q/
Q?V,
we find that:
Cnew = kCold
If the potential difference across the capacitor is too large, then the electric
field will be so strong that the electrons escape from their atoms and move
toward the positive plate. This dielectric breakdown not only discharges
the capacitor, but also burns a hole in the dielectric and ruins the capacitor.
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.