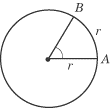
A degree is equal to 1 /360 of a circle, while a radian is equal to the
angle that intercepts an arc of the same length as the radius of the circle. In
the figure below, arc AB has length r, and the central angle
measures one radian.
When converting between the two measurement systems, use the proportion:
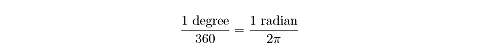
which can be simplified to:
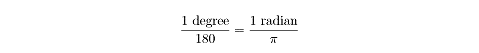
To convert from degrees to radians:
multiply the degree measure byp /180. For example, 60º is equal to60p/ 180 =
p /3 radians.
To convert from radians to degrees:
multiply the measure in radians by 180 /p. For example,
p/4 radians is equal to 180p/ 4p = 45º.
Here are the most important angle measures in degrees and radians:

On the Math IC, it is sometimes a better idea to work solely in radians, rather
than convert back and forth between radians and degrees. Using radians is
especially easy on graphing calculators that allow you to switch into radian
mode.
Back
Next
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.