Task: Select the correct answer and then click Continue.
In the figure above, if ABCD is a parallelogram,
then x =
A key feature in this figure is the line that extends from the
base of the parallelogram. This line is composed of two supplementary
angles; one is marked 50°, and the other is 
ABC.
Together, these angles must equal 180°, the degree measure of
a straight line. Therefore,
ABC measures 180° – 50° = 130°. Now
that we have handled this external angle and obtained this valuable
piece of information, we can deal with the angles of parallelogram
ABCD.
Since ABCD is a parallelogram, AB is parallel
to DC and AD is parallel to BC.
In addition, diagonal AC functions as a transversal in
this figure, cutting both sets of parallel lines at the same angle
and creating sets of equivalent angles. Therefore, we know that
ACB = DAC
= 20°, and BAC
= DCA = x.
There are now two approaches we can use to determine x:
- Adjacent angles of
a parallelogram are supplementary:
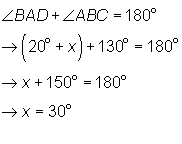
- The sum of angles
in a triangle equals 180°:
Choice (B) is correct.
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.