You have a square plot of land? (Check.) Surrounded by a fence on all sides? (Check.) A next-door neighbor (check) has a rectangular plot (okay, a square is a rectangle, check), and it's the same size and dimensions as mine. (Check, it looks just like mine.) He wants to put up a fence around his plot. I've got that here. What percentage of his fence have I completed for him already? Well, 25%. Okay, I match all of these. My diagram fulfills all of the requirements from here. So I'm good to go.
Example #2
The visual for the second example problem
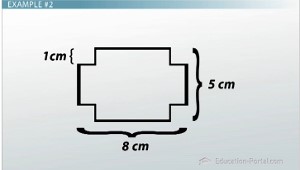
Let's do another one. Let's do a slightly harder one. We are given a paper rectangle of area 40 centimeters squared that has a width of 8 centimeters and a height of 5 centimeters (well, yes, a width of 8 centimeters and height of 5 centimeters will give me 40 centimeters squared, so I'm good.) I'm going to cut 1-centimeter squares from each of the four corners. Then I'm going to fold up each side to make an open box. What is the volume of the box?
This sounds a little bit more complex, but let's remember our keys. First, I'm going to pull out important information. Okay, important information: It's a rectangle. I don't know if I'm going to need this 40 centimeters squared, so I'm not exactly going to include that, but I'm going to keep in my head that I know that. So I've got a rectangle. It's got a width of 8 centimeters and a height of 5 centimeters, and I'm going to cut 1-centimeter squares from each of the corners. Let's start with that. Here's my rectangle. It's 8 centimeters wide and 5 centimeters tall. I'm going to cut 1-centimeter squares from each corner. That sounds about right, and there, the corners are gone. Hmm. If I just cut 1 centimeter off each of the corners, then I know that the whole width is still going to be 8 centimeters, but the width at the edge here is going to be 6 centimeters. Similarly, I know that the whole height is going to be 5 centimeters, but I've cut 1 centimeter from each side, and so the height right here is going to be 3 centimeters.
Now I'm going to fold up each side to make an open box. So here's my 3 by 6, and I'm going to fold up each side. I'm going to assume that means I should fold on these dotted lines here. If I fold here, then, this side is going to be 90 degrees from the bottom of the paper. This edge here is going to join this edge here, along one edge. Then I'm going to get a new edge where these two edges meet. Same with these two and same with these two. I'm not quite sure that this is going to work, so let's pull out a sheet of paper and actually do this. We'll rip out these corners, and let's try folding where my dotted lines would be on this diagram. Okay, this looks like an open box. What are the dimensions of this box? The width is going to be, now, 6 centimeters because we had 8 centimeters and we took off 1 on each side. So we've got 6 centimeters. The height from my sheet of paper is going to become the depth of the box, and that's now 3 centimeters, because we've folded up the front and the back. And the height is going to be 1 centimeter. That's from these boxes, these rectanglesthat we cut out. So now I have a box that's 3 centimeters by 6 centimeters by 1 centimeter. If you know how to find the volume of a box, then you would know that the whole volume of this is going to be 1 * 3 * 6. So that's 18 centimeters cubed.
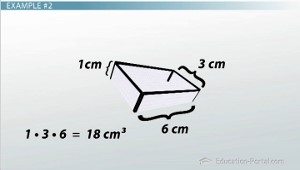
Finding the volume in example #2
We drew it out. What's more, we actually took a sheet of paper and folded it up to see. We needed some help here. It's 3-D, why not? Let's check our results. Do we actually match all of the requirements? We had a paper rectangle. There's one sitting on the floor here. That rectangle, at least in our diagram, had an area of 40 centimeters squared. It had a width of 8 centimeters and a height of 5 centimeters. All sounds great so far. I cut 1-centimeter squares from the each of the corners, yes, and I folded up each side and made an open box. I wasn't exactly sure if I knew where to fold it, but I folded up each side to make an open box, so I fulfilled the requirement. Then I found the volume of the box, and it made sense.
Lesson Summary
There are a few keys with visualization that you should always remember. One, you want to pull out all of the important information. And when you're done with the problem, you need to look at that important information and make sure that your solution satisfied all of those bits. This is like the origami. You know at the end, you need to have a head on your origami crane. If your origami crane doesn't have a head, then you probably didn't solve it correctly.
You also want to, as best as possible, draw it out. If you have something that's 3-D, drawing it out might mean that you draw it on a sheet of paper, but then you actually try to use your hands to make whatever you need. In this case, we made an open box with a sheet of paper that we had on hand.
Finally, as I mentioned before, always check your results. You need to think, does this make sense? If we had a volume that gave us -100 centimeters cubed, we might know there's a problem, because a volume should not be negative. So always check your results.