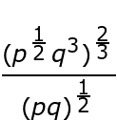
First we're going to simplify the power to a power. So now we'll have:
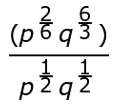
Write like terms over each other, if necessary. Well, we already have the p's over the p's and the q's over the q's. There's no need to simplify fractions now. We're going to go right to simplifying quotient of powers. Remember, when we divide, we subtract their exponents. So we have:
p(2/6 - 1/2) * q(6/3 - 1/2)
That gives us:
p(-1/6) * q(9/6)
Next we need to reduce the fractions because we're almost to our answer. So we'll have:
p(-1/6) * q(3/2)
We want to rewrite these using positive exponents. Remember, if it's negative in the numerator, it flips to the denominator. So our final answer's going to be:
q(3/2) / p(1/6)
Example #6

The solution for example 6 after applying the quotient of powers property
Simplify using positive exponents. Always reduce the fractions to lowest terms. We're going to have:
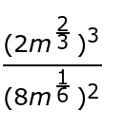
We're going to simplify power to a power. So we'll have:
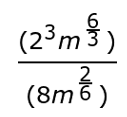
Remember, power to a power means to multiply the exponents. Next, let's write like terms over each other. We already have 23 over 82 and m(6/3) over m(2/6). So let's move to the next step. There's no need to simplify fractions just yet, so we're going to simplify quotient of powers. Remember, when we divide, we subtract. So now we're going to have:
8/64 * m(6/3 - 2/6)
Well, 8/64 is 1/8. m to the 6/3 - 2/6 is m to the 10/6. So it turns out that our final answer is:
m(5/3) / 8
We won't touch the improper fraction in this video. We're just simplifying rational exponents.
Example #7
Simplify using positive exponents. Always reduce fractions to lowest terms.
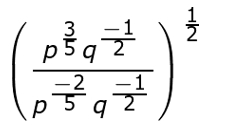
First we're going to simplify power to a power. Remember, power to a power means to multiply the exponents. That'll give us:
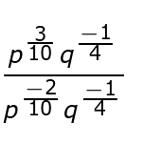
Next, if we need to, write like terms over each other. There's no need to simplify fractions now. We're going to move to quotient of powers. Remember, when we divide, we subtract their exponents. So that's going to give us:
p(3/10 - (-2/10))q(-1/4 - (-1/4))
So let's keep simplifying.
p(5/10)q(0)
The zero exponent says q0 equals 1. Now we need to reduce our fraction 5/10. That's going to give us our answer:
p(1/2)

The radical to rational fraction formula used in example 8
Radical to Rational Fraction Formula
Review radical to rational fraction formula...
The bth root of xa = x(a/b)
The index is the denominator. The exponent is the numerator. What happens when the expression has radicals?
- Change the radicals to rational exponents
- Follow exponent rules
Example #8
(third root of x)(fifth root of x4)
First we need to change to rational exponents, so we're going to have:
x(1/3) * x(4/5)
Did you remember the denominator is the index number and the numerator is the radicand exponent? Following our exponent rules, we're going to do a product of powers. Remember, when we multiply, we add their exponents. So we're going to have:
x(1/3 + 4/5)
Well, 1/3 plus 4/5 is 17/15. So our answer's going to be:
x(17/15)
Remember, we need to change the rational exponent back into a radical expression.
x(17/15) = 15th root of x17
Lesson Summary
Rational exponents follow the exponent rules. Remember to reduce fractions as your final answer, but you don't need to reduce until the final answer. For operations on radical expressions, change the radical to a rational expression, follow the exponent rules, then change the rational expression back to a radical expression.