1) m2 = n2 + n + m
2) n2 = m2 - 2m + 1
m
=
m =
1) 
| |
 |
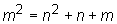
Sufficient |
 |
Insufficient |
|
|
If m and n are consecutive, then
we can replace m in the expression with one of n –
1 or n + 1 without violating the equation. If they’re not, the
equation won’t work if we do so. So, let’s try n – 1:
Is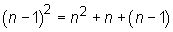 
?
Well, if we work out both sides of the equation, we get 
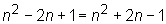. These are not equal, so we know that 
.
Now let’s try n + 1:
Is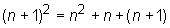 
?
Well, if we work out both sides of the equation, we get 
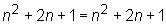. These are equal, so we know that m = n
+ 1, which means that m and n are indeed consecutive. Statement
1 is therefore sufficient.
Let’s look at Statement 2.
v>
Countinue
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ