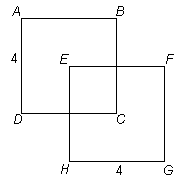
What is the area of the region in which squares ABCD
and EFGH overlap?
1) F bisects BC
2) 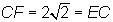
- What do we know about the two figures and the overlapping
area?
- What are we unable to determine about the two figures
and the overlapping area?
1) EF bisects BC
| |

|
Sufficient |
 |
Insufficient |
|
|
2) 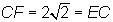
| |

|
Sufficient |

|
Insufficient |
|
|
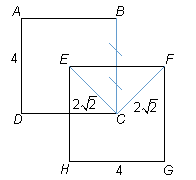
1) EF bisects BC
2) 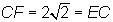
| |

|
Sufficient |

|
Insufficient |
|
|
Countinue
If EF bisects BC, we know that the distance from the point
of intersection to point C must be 2. We know from Statement 2
that the distance from point C to points E and F
is 2v. Since the distances
between point C and points E and F are equal, BC
must also bisect EF. This means that the triangle formed by the
left half of EF, the bottom half of BC and the line segment
CE has side lengths of 2, 2 and 2v. In other words, it’s a right isosceles triangle.
So EF must be perpendicular to BC.
We also know that since EFGH and ABCD are both squares
and have right angles, the other two sides of the overlap must be perpendicular
as well. So the quadrilateral overlap is indeed a square with sides of
length 2, and the area of the overlap must be 4. The two statements are
sufficient in combination.
Let’s try an algebra question:
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ