Take a look at this question. Again, the first thing
we’ll do is evaluate the question stem.
If a and b are positive integers and a
+ b > ab, what is the value of a?
1) 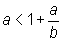
2) ab ? a
This question is testing
rules.
Countinue
Normally, the product of two positive integers is greater than their
sum (e.g., 5 ×
2 > 5 + 2), so a statement like a + b > ab
should immediately make you wonder what possible values of a and/or
b could make this inequality true. Once again, let's think about
the likely suspects: 0, 1 and –1.
We know from the question stem that both a and b are positive,
so that scratches 0 and –1. But what about 1? Let’s try out a few examples:
1 + 1 > 1 × 1
1 + 2 > 1 ×
2
1 + 3 > 1 ×
3
Notice that these inequalities are all true. Also note that the question
stem didn’t prohibit the possibility that a and b could
have the same value. So either a or b (or maybe both) must
equal 1 in order for the inequality a + b > ab
to be true.
Aha! Now we can see the real question here: Is a = 1? That’s what
we’ll be looking for as we evaluate each statement.
Countinue
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ