Lesson: Chapter - 8

Pendulums

A pendulum is defined as a mass, or bob, connected to a rod or rope, that experiences simple harmonic motion as it swings back and forth without friction. The equilibrium position of the pendulum is the position when the mass is hanging directly downward.

Consider a pendulum bob connected to a massless rope or rod that is held at an angle ?_max from the horizontal. If you release the mass, then the system will swing to position -?_max and back again.

The oscillation of a pendulum is much like that of a mass on a spring. However, there are significant differences, and many a student has been tripped up by trying to apply the principles of a spring’s motion to pendulum motion.

Properties of Pendulum Motion

As with springs, there are a number of properties of pendulum motion that you might be tested on, from frequency and period to kinetic and potential energy. Let’s apply our three-step method of approaching special problems in mechanics and then look at the formulas for some of those properties:

1. Ask yourself how the system will move: It doesn’t take a rocket scientist to surmise that when you release the pendulum bob it will accelerate toward the equilibrium position. As it passes through the equilibrium position, it will slow down until it reaches position -?, and then accelerate back. At any given moment, the velocity of the pendulum bob will be perpendicular to the rope. The pendulum’s trajectory describes an arc of a circle, where the rope is a radius of the circle and the bob’s velocity is a line tangent to the circle.
2. Choose a coordinate system: We want to calculate the forces acting on the pendulum at any given point in its trajectory. It will be most convenient to choose a y-axis that runs parallel to the rope. The x-axis then runs parallel to the instantaneous velocity of the bob so that, at any given moment, the bob is moving along the x-axis.
3. Draw free-body diagrams: Two forces act on the bob: the force of gravity, F = mg, pulling the bob straight downward and the tension of the rope, F_T, pulling the bob upward along the y-axis. The gravitational force can be broken down into an x-component, mg sin?, and a y-component, mg cos?. The y component balances out the force of tension—the pendulum bob doesn’t accelerate along the y-axis—so the tension in the rope must also be mg cos?. Therefore, the tension force is maximum for the equilibrium position and decreases with ?. The restoring force is mg sin ?, so, as we might expect, the restoring force is greatest at the endpoints of the oscillation, ? = ± ?_max and is zero when the pendulum passes through its equilibrium position.

You’ll notice that the restoring force for the pendulum, mg sin?, is not directly proportional to the displacement of the pendulum bob, ?, which makes calculating the various properties of the pendulum very difficult. Fortunately, pendulums usually only oscillate at small angles, where sin ? = ?. In such cases, we can derive more straightforward formulas, which are admittedly only approximations. However, they’re good enough for the purposes of subject test Physics.

Period

The period of oscillation of the pendulum, T, is defined in terms of the acceleration due to gravity, g, and the length of the pendulum, L:

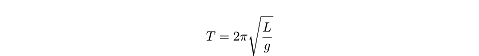
This is a pretty scary-looking equation, but there’s really only one thing you need to gather from it: the longer the pendulum rope, the longer it will take for the pendulum to oscillate back and forth. You should also note that the mass of the pendulum bob and the angle of displacement play no role in determining the period of oscillation.

Energy

The mechanical energy of the pendulum is a conserved quantity. The potential energy of the pendulum, mgh, increases with the height of the bob; therefore the potential energy is minimized at the equilibrium point and is maximized at ? = ± ?_max. Conversely, the kinetic energy and velocity of the pendulum are maximized at the equilibrium point and minimized when ? = ± ?_max.

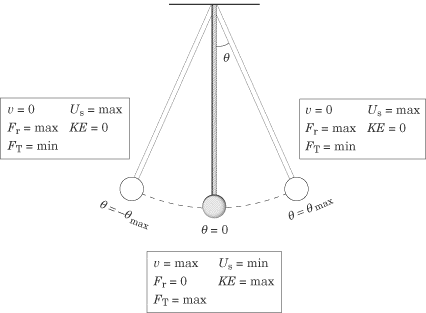
The figure below summarizes this information in a qualitative manner, which is the manner in which you are most likely to find it on subject test Physics. In this figure, v signifies velocity, F signifies the restoring force, F_T signifies the tension in the pendulum string, U signifies potential energy, and KE signifies kinetic energy.

Velocity Calculating the velocity of the pendulum bob at the equilibrium position requires that we arrange our coordinate system so that the height of the bob at the equilibrium position is zero. Then the total mechanical energy is equal to the kinetic energy at the equilibrium point where U = 0. The total mechanical energy is also equal to the total potential energy at ± ?_max where KE = 0. Putting these equalities together, we get

E = 1/2mv² = mgh

But what is h?

From the figure, we see that h = L - Lcos(-?_max) . If we plug that value into the equation above, we can solve for v:

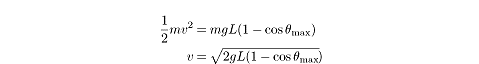
Don’t let a big equation frighten you. Just register what it conveys: the longer the string and the greater the angle, the faster the pendulum bob will move.

How This Knowledge Will Be Tested

Again, don’t worry too much about memorizing equations: most of the questions on pendulum motion will be qualitative. There may be a question asking you at what point the tension in the rope is greatest (at the equilibrium position) or where the bob’s potential energy is maximized (at ? = ± ?_max ). It’s highly unlikely that you’ll be asked to give a specific number.

Next to display next topic in the chapter.