Kinetic Energy
Kinetic energy is the energy a body in motion has by virtue of its motion. We
define energy as the capacity to do work, and a body in motion is able to use
its motion to do work. For instance, a cue ball on a pool table can use its
motion to do work on the eight ball. When the cue ball strikes the eight ball,
the cue ball comes to a stop and the eight ball starts moving. This occurs
because the cue ball’s kinetic energy has been transferred to the eight ball.
There are many types of kinetic energy, including vibrational, translational,
and rotational. Translational kinetic energy, the main type, is the
energy of a particle moving in space and is defined in terms of the particle’s
mass, m, and velocity,
v:
K.E = 1/2 mv2
For instance, a cue ball of mass 0.5 kg moving at a velocity of 2 m/s has
a kinetic energy of 1/2 (0.5 kg)(2 m/s)2 = 1 J.
The Work-Energy Theorem
If you recall, work is a measure of the transfer of energy. An object that has a
certain amount of work done on it has that amount of energy transferred to it.
This energy moves the object over a certain distance with a certain force; in
other words, it is kinetic energy. This handy little fact is expressed in the
work-energy theorem, which states that the net work done on an object is
equal to the object’s change in kinetic energy:
W = ?KE
For example, say you apply a force to a particle, causing it to accelerate.
This force does positive work on the particle and increases its kinetic energy.
Conversely, say you apply a force to decelerate a particle. This force does negative
work on the particle and decreases its kinetic energy. If you know the forces acting
on an object, the work-energy theorem provides a convenient way to calculate the
velocity of a particle.
Example
A hockey puck of mass 1 kg slides across the ice with an initial velocity
of 10 m/s. There is a 1 N force of friction acting against the puck. What is the
puck’s velocity after it has glided 32 m along the ice?
If we know the puck’s kinetic energy after it has glided 32 m, we can
calculate its velocity. To determine its kinetic energy at that point,
we need to know its initial kinetic energy, and how much that kinetic energy
changes as the puck glides across the ice.
First, let’s determine the initial kinetic energy of the puck. We know the puck’s
initial mass and initial velocity, so we just need to plug these numbers into the equation
for kinetic energy:
KE = 1/2mv2 = 1/2 (1kg)(10m/s)2 = 50J
The friction between the puck and the ice decelerates the puck.
The amount of work the ice does on the puck, which is the product of the
force of friction and the puck’s displacement, is negative.
W = F.s = (-N)(32m) = 32J
The work done on the puck decreases its kinetic energy, so after it has glided 32 m,
the kinetic energy of the puck is 50 – 32 = 18 J. Now that we know the final kinetic
energy of the puck, we can calculate its final velocity by once more plugging numbers
into the formula for kinetic energy:
KE = 1/2 mv2
18J = 1/2(1kg)v2
v2 = 36(m/s)2
v = 6m/s
We could also have solved this problem using Newton’s Second Law and some kinematics,
but the work-energy theorem gives us a quicker route to the same answer.
Potential Energy
As we said before, work is the process of energy transfer. In the example above,
the kinetic energy of the puck was transferred into the heat and sound caused by
friction. There are a great number of objects, though, that spend most of their
time neither doing work nor having work done on them. This book in your hand,
for instance, is not doing any work right now, but the second you drop
it—whoops!—the force of gravity does some work on it, generating kinetic energy.
Now pick up the book and let’s continue.
Potential energy, U, is a measure of
an object’s unrealized potential to have work done on it, and is associated with
that object’s position in space, or its configuration in relation to other
objects. Any work done on an object converts its potential energy into kinetic
energy, so the net work done on a given object is equal to the negative change
in its potential energy:
W = ?U
Be very respectful of the minus sign in this equation. It may be tempting to
think that the work done on an object increases its potential energy, but the
opposite is true. Work converts potential energy into other forms of energy,
usually kinetic energy. Remove the minus sign from the equation above, and you
are in direct violation of the law of conservation of energy!
There are many forms of potential energy, each of which is associated with a
different type of force. subject test Physics usually confines itself to gravitational
potential energy and the potential energy of a compressed spring. We will review
gravitational potential energy in this section, and the potential energy of a
spring in the next chapter.
Gravitational Potential Energy
Gravitational potential energy registers the potential for work done on an
object by the force of gravity. For example, say that you lift a water balloon
to height h above the ground. The
work done by the force of gravity as you lift the water balloon is the force of
gravity, -mg, times the water
balloon’s displacement, h. So the
work done by the force of gravity is W = –mgh.
Note that there is a negative amount of work done, since the water balloon is
being lifted upward, in the opposite direction of the force of gravity.
By doing –mgh joules of work on the
water balloon, you have increased its gravitational potential energy by
mgh joules (recall the equation
W = -?U).
In other words, you have increased its potential to accelerate downward and
cause a huge splash. Because the force of gravity has the potential to do
mgh joules of work on the water
balloon at height h, we say that the
water balloon has mgh joules of
gravitational potential energy.
U9 = mgh
For instance, a 50 kg mass held at a height of 4 m from the ground has a
gravitational potential energy of:
U9 = mgh = (50kg)(9.8m/s2)(4m) = 1960J
The most important thing to remember is that the higher an object is off the
ground, the greater its gravitational potential energy.
Mechanical Energy
We now have equations relating work to both kinetic and potential energy:
W = ? KE
W = - ?U
Combining these two equations gives us this important result:
? KE + ?U = 0
or alternatively
? KE = - ?U
As the kinetic energy of a system increases, its potential energy decreases
by the same amount, and vice versa. As a result, the sum of the kinetic energy
and the potential energy in a system is constant. We define this constant as E,
the mechanical energy of the system:
KE + U = E
This law, the conservation of mechanical energy, is one form of the more
general law of conservation of energy, and it’s a handy tool for solving problems
regarding projectiles, pulleys, springs, and inclined planes. However, mechanical
energy is not conserved in problems involving frictional forces. When friction is
involved, a good deal of the energy in the system is dissipated as heat and sound.
The conservation of mechanical energy only applies to closed systems.
Example 1
A student drops an object of mass 10 kg from a height of 5 m.
What is the velocity of the object when it hits the ground?
Assume, for the purpose of this question, that g = –10 m/s2.
Before the object is released, it has a certain amount of gravitational
potential energy, but no kinetic energy. When it hits the ground, it has no
gravitational potential energy, since h = 0, but it has a certain amount of
kinetic energy. The mechanical energy, E, of the object remains constant, however.
That means that the potential energy of the object before it is released is equal
to the kinetic energy of the object when it hits the ground.
mgh = (10kg)(-10m/s2)(-5m) = 500J
By the time it hits the ground, all this potential energy will have
been converted to kinetic energy. Now we just need to solve for v:
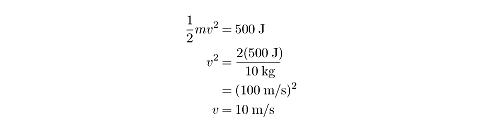
Example 2

Consider the above diagram of the trajectory of a thrown tomato:
- At what point is the potential energy greatest?
- At what point is the kinetic energy the least?
- At what point is the kinetic energy greatest?
- At what point is the kinetic energy decreasing and the potential energy increasing?
- At what point are the kinetic energy and the potential energy equal to the
values at position A?
The answer to question 1 is point B. At the top of the tomato’s trajectory, the
tomato is the greatest distance above the ground and hence has the greatest
potential energy.
The answer to question 2 is point B. At the top of the tomato’s trajectory, the
tomato has the smallest velocity, since the y-component of the velocity is zero,
and hence the least kinetic energy. Additionally, since mechanical energy is
conserved in projectile motion, we know that the point where the potential
energy is the greatest corresponds to the point where the kinetic energy is
smallest.
The answer to question 3 is point E. At the bottom of its trajectory, the tomato
has the greatest velocity and thus the greatest kinetic energy.
The answer to question 4 is point A. At this point, the velocity is decreasing
in magnitude and the tomato is getting higher in the air. Thus, the kinetic
energy is decreasing and the potential energy is increasing.
The answer to question 5 is point C. From our study of kinematics, we know that
the speed of a projectile is equal at the same height in the projectile’s ascent
and descent. Therefore, the tomato has the same kinetic energy at points A and
C. Additionally, since the tomato has the same height at these points, its
potential energy is the same at points A and C.
Keep this example in mind when you take subject test Physics, because it is likely
that a similar question will appear on the test.
Thermal Energy
There are many cases where the energy in a system seems simply to have
disappeared. Usually, this is because that energy has been turned into sound and
heat. For instance, a coin sliding across a table slows down and comes to a
halt, but in doing so, it produces the sound energy of the coin scraping along
the table and the heat energy of friction. Rub your hands together briskly and
you will feel that friction causes heat.
We will discuss thermal energy, or heat, in greater detail in Chapter 9, but
it’s worth noting here that it is the most common form of energy produced in
energy transformations. It’s hard to think of an energy transformation where no
heat is produced. Take these examples:
- Friction acts everywhere, and friction produces heat.
- Electric energy produces heat: a light bulb produces far more heat than it does
light.
- When people talk about burning calories, they mean it quite literally: exercise
is a way of converting food energy into heat.
- Sounds fade to silence because the sound energy is gradually converted into the
heat of the vibrating air molecules. In other words, if you shout very loudly,
you make the air around you warmer!
Back
Next
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.