Electric Potential Energy
Because an electric field exerts a force on any charge in that field, and
because that force causes charges to move a certain distance, we can say that an
electric field does work on charges. Consequently, we can say that a charge in
an electric field has a certain amount of potential energy,
U. Just as we saw in the chapter on
work, energy, and power, the potential energy of a charge decreases as work
is done on it:
?U = -W
Work
The work done to move a charge is the force, F,
exerted on the charge, multiplied by the displacement,
d, of the charge in the direction of
the force. As we saw earlier, the magnitude of the force exerted on a charge
q in an electric field
E is
Fq
= qE. Thus, we can derive the following equation for the
work done on a charge:
W = qED
Remember that d is not simply the
displacement; it is the displacement in the direction that the force is exerted.
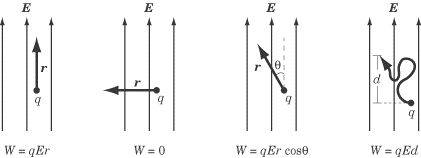
When thinking about work and electric fields, keep these three rules in mind:
- When the charge moves a distance r
parallel to the electric field lines, the work done is
qEr.
- When the charge moves a distance r
perpendicular to the electric field lines, no work is done.
- When the charge moves a distance r
at an angle
?
to the electric field lines, the work done is qEr
cos?
.
Example
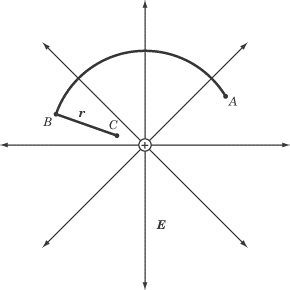
In an electric field, E, a
positive charge, q, is moved in the circular path described above, from
point A to point B, and then in a straight line of distance r
toward the source of the electric field, from point B to point C.
How much work is done by the electric field on the charge? If the charge were
then made to return in a straight line from point C to point A,
how much work would be done?
How much work is done moving the charge from point A to point B to
point C??
The path from point A to point
B is perpendicular to the radial
electric field throughout, so no work is done. Moving the charge from point
B to point
C requires a certain amount of work
to be done against the electric field, since the positive charge is moving
against its natural tendency to move in the direction of the electric field
lines. The amount of work done is:
W = -qEr
The negative sign in the equation reflects the fact that work was done against
the electric field.
How much work is done moving the charge directly from point C back to
point A?
The electric force is a conservative force, meaning that the path taken from one
point in the electric field to another is irrelevant. The charge could move in a
straight line from point C to point
A or in a complex series of zigzags:
either way, the amount of work done by the electric field on the charge would be
the same. The only thing that affects the amount of work done is the
displacement of the charge in the direction of the electric field lines. Because
we are simply moving the charge back to where it started, the amount of work
done is W = qEr.
Potential Difference
Much like gravitational potential energy, there is no absolute, objective point
of reference from which to measure electric potential energy. Fortunately, we
are generally not interested in an absolute measure, but rather in the electric
potential, or potential difference, V,
between two points. For instance, the voltage reading on a battery tells us the
difference in potential energy between the positive end and the negative end of
the battery, which in turn tells us the amount of energy that can be generated
by allowing electrons to flow from the negative end to the positive end. We’ll
look at batteries in more detail in the chapter on circuits.
Potential difference is a measure of work per unit charge, and is measured in
units of joules per coulomb, or volts (V). One volt is equal to one joule
per coulomb.
V = W/q
Potential difference plays an important role in electric circuits, and we will
look at it more closely in the next chapter.
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.