Lesson: Chapter - 7

Prisms

Most of the solids you’ll see on the Subject Math  test are prisms, or variations on prisms. A prism is defined as a geometric solid with two congruent bases that lie in parallel planes. You can create a prism by dragging any two-dimensional triangle, circle, or polygon through space without rotating or tilting it. The three-dimensional space defined by the moving triangle or polygon is the body of the prism. The prism’s two bases are the planes where the two-dimensional shape begins and ends. The perpendicular distance between the bases is the height of the prism.

The figures below are all prisms. The bases of these prisms are shaded, and the altitude (the height) of each prism is marked by a dashed line:

There are two main aspects of geometric solids that are relevant for the Subject Math : volume and surface area.

Volume of a Prism

The volume of a prism is the amount of space taken up by that prism. The general formula for calculating the volume of a prism is very simple:

Volume = Bh

where B is the area of the base, and h is the prism’s height. Certain geometric solids have slightly different formulas for calculating volume that we will cover on a case-by-case basis.

Surface Area

The surface area of a prism is the sum of the areas of all the prism’s sides. The formula for the surface area of a prism therefore depends on the type of prism with which you are dealing. As with volume, we cover the specifics of calculating surface area as we cover each type of geometric solid.

Rectangular Solids

A rectangular solid is a prism with a rectangular base and lateral edges that are perpendicular to its base. In short, a rectangular solid is shaped like a box.

A rectangular solid has three important dimensions: length (l, width (w), and height (h). If you know these measurements, you can find the solid’s surface area, volume, and diagonal length.

Volume of a Rectangular Solid

The volume of a rectangular solid is given by the following formula:

Volume = lwh

where l is the length, w is the width, and h is the height. Notice how this formula corresponds with the general formula for the volume of a prism: the product lw is the area of the base. Now try to find the volume of the prism in the following example:

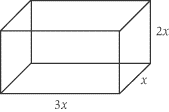
In this solid, l = 3x,w = x, and h = 2x. Simply plug the values into the formula given for volume, and you would find Volume = (3x)(2x)(x) = 6x³.

Surface Area

The surface area of a rectangular solid is given by the following formula:

Surface Area = 2lw +2lh+ 2wh

where l is the length, w is the width, and h is the height.

The six faces of a rectangular solid consist of three congruent pairs. The surface area formula is derived by simply adding the areas of the faces—two faces have areas of l × w, two faces have areas of l × h, and two faces have areas of w × h.

To practice, try to find the surface area of the rectangular solid we used as an example for volume. Here’s the figure again:

All you have to do is enter the given values into the formula for surface area:

Diagonal Length of a Rectangular Solid

The diagonal of a rectangular solid, d, is the line segment whose endpoints are opposite corners of the solid. Every rectangular solid has four diagonals, each with the same length, that connect each pair of opposite vertices. Here’s one diagonal drawn in:

The formula for the length of a diagonal is:

where l is the length, w is the width, and h is the height.

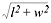
You can look at this formula as the Pythagorean theorem in three dimensions. In fact, you can derive this formula using the Pythagorean theorem. First, find the length of the diagonal along the base. This is . Then use the Pythagorean theorem again, incorporating height to find the length of the diagonal from one corner to the other:
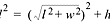
Thus,

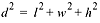
and

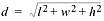
A Math IC question might ask you:

What is the length of diagonal AH in the rectangular solid below if AC = 5, GH = 6, and CG = 3?

The question gives the length, width, and height of the rectangular solid, so you can just plug those numbers into the formula:

The length of the diagonal AH (as well as BG, CF, and DE) is v7.

Cubes

Just as a square is a special kind of rectangle, a cube is a special kind of rectangular solid. A cube is a rectangular solid whose edges are each the same length. In other words, the length, width, and height are equal, and each of its six faces is a square.

Volume of a Cube

The formula for finding the volume of a cube is essentially the same as the formula for the volume of a rectangular volume. However, since a cube’s length, width, and height are all equal, the cube volume formula is:

Volume of a Cube = 8³
where s is the length of one edge of the cube.

Surface Area of a Cube

Since a cube is just a rectangular solid whose sides are all equal, the formula for finding the surface area of a cube is the same as that for a rectangular solid, except with s = l = w = h:

Surface Area of a Cube = 6₈²
where s is the length of one edge of the cube.

Diagonal Length of a Cube

The same is true for measuring the diagonal length of a cube. The formula for the diagonal of a cube is simply adapted from the formula for the diagonal length of a rectangular solid, with s = l = w = h:

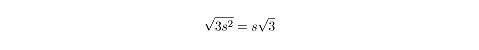
where s is the length of one edge of the cube.

Cylinders

A cylinder is a prism with circular bases.

The height of a cylinder, h, is the length of the line segment whose endpoints are the centers of the bases. The radius of a cylinder, r, is the radius of its base. If you know the height and radius of a cylinder, you can easily calculate its volume and surface area.

Volume of a Cylinder

The volume of a cylinder is the product of the area of its base and its height. Because a cylinder has a circular base, the volume of a cylinder is:

Volume of a Cylinder = pr²h

where r is the radius of the circular base and h is the height. Try to find the volume of the cylinder below:

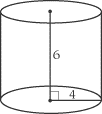
This cylinder has a radius of 4 and a height of 6. Using the volume formula:
Volume = p(4)² (6) = 96p

Surface Area of a Cylinder

The surface area of a cylinder is the sum of the areas of the two bases and the lateral face of the cylinder. The bases are congruent circles, so their areas can be found easily. The lateral face is the tubing that connects the two bases. When “unrolled,” the lateral base is simply a rectangle whose length is the circumference of the base and whose width is the height of the cylinder. Therefore, the surface area of a cylinder is given by this formula:

Surface Area = 2pr² + 2prh

where r is the radius and h is the height. As with finding the volume of a cylinder, finding the surface area involves plugging the height and radius of the base into the formula. To find the surface area of the cylinder in the practice example on volume,

just plug the values into the formula:
Surface Area = 2p(4)² + 2p(4)(6)
= 32p + 48p
= 80 p
Back Next

Next to display next topic in the chapter.

Mathematics Practice Questions