Lesson: Chapter - 5

Common Word Problems

The writers of the Math IC love word problems. These problems force you to show your range as a mathematician. They demand that you read and comprehend the problem, set up an equation or two, and manipulate the equations to find the solution. Luckily, the Math IC uses only a few types of word problems, and we have the nitty-gritty on all of them.

v>

Rates

A rate is a ratio of related qualities that have different units. For example, speed is a rate that relates the two quantities of distance and time. Here is the general rate formula:

quantity A ( in x units ) × rates (in y/x units) = quantity B ( in y units)

No matter the specifics, the key to a rate problem is correctly placing the given information in the three categories. Then, you can substitute the values into the rate formula. We’ll look at the three most common types of rate: speed, work, and price.

Speed

In the case of speed, time is quantity a and distance is quantity b. For example, if you traveled for 4 hours at 25 miles per hour, then:

4 hours × 25 miles/hours = 100 miles

Note that the hour units canceled out, since the hour in the rate is at the bottom of the fraction. But you can be sure that the Math IC test won’t simply give you one of the quantities and the rate and ask you to plug it into the rate formula. Because rate questions are in the form of word problems, the information that you’ll need to solve the problem will often be given in a less straightforward manner.

Here’s an example:

Jim rollerblades 6 miles per hour. One morning, Jim starts rollerblading and doesn’t stop until he has gone 60 miles. How many hours did he rollerblade?

This question provides more information than simply the speed and one of the quantities. We know unnecessary facts such as how Jim is traveling (by rollerblades) and when he started (in the morning). Ignore them and focus on the facts you need to solve the problem.

• Time a: x hours rollerblading
• Rate: 6 miles per hour
• Quantity b: 60 miles

So, we can write: x hours for rollerblading = 60 miles ÷ 6 miles per hour = 10 hours

Jim was rollerblading for 10 hours. This problem requires a little analysis, but basically we plugged some numbers into the rate equation and got our answer. Here’s a slightly more difficult rate problem:

At a cycling race, there are 50 cyclists in all, each representing a state. The cyclist from California can cumulatively cycle 528,000 feet per hour. If the race is 480 miles long, how long will it take him to finish the race?

Immediately, you should pick out the given rate of 528,000 feet per hour and notice that 480 miles are traveled. You should also notice that the question presents a units problem: the given rate is in feet cycled per hour, and the distance traveled is in miles.

Sometimes a question will give you inconsistent units, like in this example. Always read over the problem carefully and don’t forget to adjust the units—the answer choices are bound to include non-adjusted options, just to throw you off.

For this question, since we know there are 5,280 feet in a mile, we can find the rate for miles per hour:

528,000feet per hours ÷ 5280 miles per hour = 100 miles per hour

We can now plug the information into the rate formula:

• Time: x hours cycling
• Rate: 100 miles per hour
• Distance: 480 miles

480 miles ÷ 100 miles per hour = 4.8 hours So it takes the cyclist 4.8 hours to finish the race.

Work

In work questions, you will usually find the first quantity measured in time, the second quantity measured in work done, and the rate measured in work done per time. For example, if you knitted for 8 hours and produced two sweaters per hour, then:

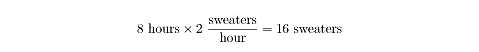
Here is a sample work problem. It is one of the harder rate questions you might come across on the Math IC:

Four men can dig a 40 foot well in 4 days. How long would it take for 8 men to dig a 60 foot well? Assume that these 8 men work at the same pace as the 4 men.

First, let’s examine what that problem says: 4 men can dig a 40 foot well in 4 days. We are given a quantity of work of 40 feet and a time of 4 days. We need to create our own rate, using whichever units might be most convenient, to carry over to the 8-men problem. The group of 4 men dig 40 feet in 3 days. Dividing 40 feet by 4 days, you find that the group of 4 digs at a pace of 10 feet per day.

From the question, we know that 8 men dig a 60 foot well. The work done by the 8 men is 60 feet, and they work at a rate of 10 feet per day per 4 men. Can we use this information to answer the question? Yes. The rate of 10 feet per day per 4 men converts to 20 feet per day per 8 men, which is the size of the new crew. Now we use the rate formula:

• Time: x days of work
• Rate: 20 feet per day per eight men
• Total Quantity: 60 feet

60 feet ÷ 20 feet per dayb per 8 man =3 days of work for 8 man

This last problem required a little bit of creativity—but nothing you can’t handle. Just remember the classic rate formula and use it wisely.

Price

In rate questions dealing with price, you will usually find the first quantity measured in numbers of items, the second measured in price, and the rate in price per item. Let’s say you had 8 basketballs, and you knew that each basketball cost $25 each:

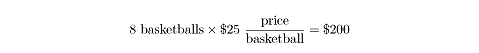
Percent Change

In percent-change questions, you will need to determine how a percent increase or decrease affects the values given in the question. Sometimes you will be given the percent change, and you will have to find either the original value or new value. Other times, you will be given one of the values and be asked to find the percent change. Take a look at this sample problem:

A professional golfer usually has an average score of 72, but he recently went through a major slump. His new average is 20 percent worse (higher) than it used to be. What is his new average?

This is a percent-change question in which you need to find how the original value is affected by a percent increase. First, to answer this question, you should multiply 72 by .20 to see what the change in score was:

72 × .20 = 14.4

Once you know the score change, then you should add it to his original average, since his new average is higher than it used to be:

72 + 14.4 = 86.4

It is also possible to solve this problem by multiplying the golfer’s original score by 1.2. Since you know that the golfer’s score went up by twenty percent over his original score, you know that his new score is 120% higher than his old score. If you see this immediately, you can skip a step and multiply 72 × 1.2 = 86.4.

Here’s another example of a percent-change problem:

A shirt whose original price was 20 dollars has now been put on sale for 14 dollars. By what percentage did its price drop?

In this case, you have the original price and the sale price and need to determine the percent decrease. All you need to do is divide the amount by which the quantity changed by the original quantity. In this case, the shirt’s price was reduced by 20 – 14 = 6 dollars. So, 6 ÷ 20 = .3, a 30% drop in the price of the shirt.

Double Percent Change

A slightly trickier version of the percent-change question asks you to determine the cumulative effect of two percent changes in the same problem. For example:

A bike has an original price of 300 dollars. Its price is reduced by 30%. Then, two weeks later, its price is reduced by an additional 20%. What is the final sale price of the bike?

One might be tempted to say that the bike’s price is discounted 30% + 20% = 50% from its original price, but the key to solving double percent-change questions is to realize that each percentage change is dependent on the last. For example, in the problem we just looked at, the second percent decrease is 20 percent of a new, lower price—not the original amount. Let’s work through the problem carefully and see. After the first sale, the price of the bike drops 30 percent:

300 -( 30 % of 300 )= 300 - .3 (300) = 300 -90 = 210 dollars

The second reduction in price knocks off an additional 20 percent of the sale price, not the original price:

210 -( 20 % of 210 )= 210 - .2 (210) = 210 -42 = 168 dollars The trickiest of the tricky percentage problems go a little something like this:

A computer has a price of 1400 dollars. Its price is raised 20%, and then lowered 20%. What is the final selling price of the computer?

If this question sounds too simple to be true; it probably is. The final price is not the same as the original. Why? Because after the price was increased by 20 percent, the reduction in price was a reduction of 20 percent of a new, higher price. Therefore, the final price will be lower than the original. Watch and learn:

1400 + ( 20% of 1400)= 1400 + .2 (1400) = 1400 + 280 =1680 dollars Now, after the price is reduced by 20%: 1680 - (20% of of 1680) = 1680 - .2 (1680) = 1680 - 336 = 1344 dollars

Double percent problems can be more complicated than they appear. But solve it step by step, and you’ll do fine.

Exponential Growth and Decay

These types of word problems take the concept of percent change even further. In questions involving populations growing in size or the diminishing price of a car over time, you need to perform percent-change operations repeatedly. Solving these problems would be time-consuming without exponents. Here’s an example:

If a population of 100 grows by 5% per year, how great will the population be in 50 years?

To answer this question, you might start by calculating the population after one year:

100 + 0.05 × 100 = 5 + 100 = 105 Or use the faster method we discussed in percent increase: 1.o5 × 100 = 105 After the second year, the population will have grown to: 100 × 1.o5 × 1.o5 = 100 × 1.o5 ² = 110.25

And so on and so on for 48 more years. You may already see the shortcut you can use to avoid having to do, in this case, 50 separate calculations. The final answer is simply:

100 × 1.o5 ⁵⁰ = 1146.74 ˜ 1147

In general, quantities like the one described in this problem are said to be growing exponentially. The formula for calculating how much an exponential quantity will grow in a specific number of years is:

Exponential decay is mathematically equivalent to negative exponential growth. But instead of a quantity growing at a constant percentage, the quantity shrinks at a constant percentage. Exponential decay is a repeated percent decrease. That is why the formulas that model these two situations are so similar. To calculate exponential decay:

final amount = origional amount × 1 - decay rate ^{(number of charges)}

The only difference between the two equations is that the base of the exponent is less than 1, because during each unit of time the original amount is reduced by a fixed percentage. Exponential decay is often used to model population decreases, as well as the decay of physical mass.

Let’s work through a few example problems to get a feel for both exponential growth and decay problems.

Simple Exponential Growth Problems

A population of bacteria grows by 35% every hour. If the population begins with 100 specimens, how many are there after 6 hours?

The question, with its growing population of bacteria, makes it quite clear that this is an exponential growth problem. To solve the problem, you just need to plug the appropriate values into the formula for a repeated percent increase. The rate is .035, the original amount is 100, and the time is 6 hours:

100 × 1.35⁶˜ 605 spceeimens

Simple Exponential Decay Problem

A fully inflated beach ball loses 6% of its air every day. If the beach ball originally contains 4000 cubic centimeters of air, how many cubic centimeters does it hold after 10 days?

Since the beach ball loses air, we know this is an exponential decay problem. The decay rate is .06, the original amount is 4000 cubic centimeters of air, and the time is 10. Plugging the information into the formula:

4000 × (.94) ¹⁰˜ 2154 cubic centimeters

More Complicated Exponential Growth Problem

A bank offers a 4.7% interest rate on all savings accounts, compounded monthly. If 1000 dollars is initially put into a savings account, how much money will the account hold two years later?

This problem is a bit tricky for the simple reason that the interest on the account is compounded monthly. This means that in the 2 years that question refers to, there will be 2 × 12 = 24 compoundings of interest. The time variable in the equation is affected by these monthly compoundings: it will be 24 instead of 2. Thus, our answer is:

1000 × 1.047²⁴ ˜ 3011.07 dollars Here’s another compounding problem:

Sam puts 2000 dollars into a savings account that pays 5% interest compounded annually. Chris puts 2500 dollars into a different savings account that pays 4% annually. After 15 years, whose account will have more money in it, if no more money is added or subtracted from the principal?

Sam’s account will have $2000 × 1.05¹⁵ ˜ $4157.85 in it after 15 years. Chris’s account will have $2500 × 1.04¹⁵ ˜ $4502.36 in it. So, Chris’s account will still have more money in it after 15 years. Notice, however, that Sam’s account is gaining on Chris’s account.

Next to display next topic in the chapter.

Mathematics Practice Questions