Applications of Similar Triangles
Similar triangles are used to solve problems in everyday situations. Learn how to solve with similar triangles here, and then test your understanding with a quiz.
Using Similar Triangles
Sarah is standing outside next to a flagpole. The sun casts a 4 ft. shadow of Sarah and a 7 ft. shadow of the flagpole. If Sarah is 5 ft. tall, how tall is the flagpole?
Without a ladder and measuring stick, you may think that solving this problem is impossible. However, finding the solution may be easier than you think. For this problem, and others like it, solving becomes a matter of similar triangles.
In another lesson, we learned that similar triangles have congruent corresponding angles and proportional corresponding sides and can be quickly identified by the Angle-Angle (AA), Side-Angle-Side (SAS), and Side-Side-Side (SSS) similarity theorems. To solve with similar triangles, we will use their side lengths to set up proportions, meaning that we will create fractions for the corresponding sides and set them equal to each other. Let's begin our practice with some basic examples.
Solving with Similar Triangles
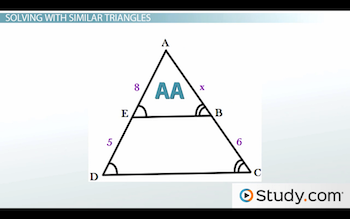
Example triangles ABE and ACD
Take a look at triangle ABE and triangle ACD above. From the picture, we see that Angle B is congruent to Angle C and Angle E is congruent to Angle D. Therefore, these triangles are similar by AA. Let's set up our proportions.
By going in the same order for each fraction, our beginning proportion is 8/5 = x/6. To get x by itself, we must cross-multiply, which will give us 5x = 48. Next, we will divide both sides by 5 to conclude that x = 9.6.
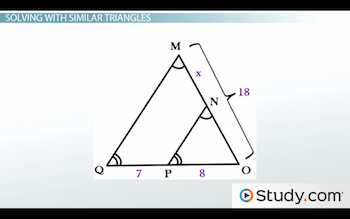
Example triangles MOQ and NOP
Here's another one: This time, we have triangle MOQ and triangle NOP. Once again, based on the congruent marks in the picture above, we know that these two triangles are similar by AA. So, let's start the problem.
In the figure, we were given the length of side MO, meaning that we also need the length of side QO for the proportion. But, we were not given this information, so we must calculate it.
To get the length of QO, we must add QP + PO since these two pieces form segment QO. By doing this, we add 7 + 8 to see that QO = 15. Now, we are ready for our proportion.
By going in the same order, our proportion is 7/15 = x/18. Then, when we cross-multiply, we see that 15x = 126. Once we divide both sides by 15, we can conclude that x = 8.4.
Applications of Similar Triangles
Now that we've covered some of the basics, let's do some real-world examples, starting with Sarah and the flagpole. Recall that Sarah is 5 ft. tall and has a 4 ft. shadow, and we are looking for the height of the flagpole, which has a 7 ft. shadow.